The New Drawing on the Right Side of the Brain (36 page)

One of the problems of seeing comes from the brain’s ability to change visual information for the purpose of fitting incoming information to pre-existing concepts or beliefs. The parts that are important (that is, provide key information), or the parts that we decide are larger, or the parts that we think should be larger, we see as larger than they actually are. Conversely, parts that are unimportant, or that we decide are smaller, or that we think should be smaller, we see as being smaller than they actually are.

Let me give you a couple of examples of this perceptual phenomenon. Figure 9-1 shows a diagrammatic landscape with four men. The man at the far right appears to be the largest of the four. But all four figures are exactly the same size. Lay a pencil alongside first the left-hand man and the right-hand man to measure and test the validity of that statement. Even after measuring and proving to yourself that the figures are the same size, however, you will probably find that the man on the right will still look larger (Figure 9-2, 9-3).

The reason for this misperception of proportionate size probably derives from our past knowledge and experience of the effect of distance on the apparent size of forms: Given two objects of the same size, one nearby and one at a distance away, the distant object will appear to be smaller. If they look the same size, the far object must be a great deal larger than the near object. This makes sense, and we don’t quarrel with the concept. But coming back to the drawing, apparently the brain enlarges the far object to make the concept truer than true. This is overdoing it! And this is precisely the kind of overdoing—of overlaying memorized verbal concepts onto visual perceptions—that causes problems with proportion for beginning drawing students.

Even after we have measured the men in the drawing and have determined with irrefutable evidence that they are the same size, we still wrongly see the right-hand man as being larger than the left. On the other hand, if you turn this book upside down and view the drawing in the inverted orientation that the verbal, conceptual mode apparently rejects, you will find that you can more easily see that the two men are the same size. The same visual information triggers a different response. The brain, apparently now less influenced by the verbal concept of diminishing size in distant forms, allows us to see the proportion correctly.

For an even more striking example of perceptual illusion, look at the drawing of two tables, Figure 9-4. Will you believe me that the two tabletops are exactly the same shape and size? You may have to use your plastic Picture Plane and trace one of the tabletops, then slide the Plane over the other tabletop to believe this. This wonderfully original illusion drawing is by Roger N. Shepard, a renowned psychologist of perception and cognition.

One more example: Stand in front of a mirror at about arm’s distance away. How large would you say is the image of your head in the mirror? About the same size as your head? Using a felt-tip pen or a crayon, extend your arm and make two marks on the mirror—one at the top of the reflected image (the outside contour of your head) and one at the bottom contour of your chin (Figure 9-5). Step to one side to see how long the image is in inches. You’ll find it’s about four and one half to five inches, or one-half the true size of your head. Yet, when you remove the marks and look again at yourself in the mirror, it seems that the image must be life-size! Again, you are seeing what you believe, not believing what you see.

Once we have accepted that the brain is changing information and not telling us that it has done so, some of the problems of drawing become clearer, and learning to see what is actually “out there” in the real world becomes very interesting. Note that this perceptual phenomenon is probably essential to ordinary life. It reduces the complexity of incoming data and enables us to have stable concepts. The problems start when we try to see what is really “out there,” for purposes of checking reality, solving real problems, or drawing realistically. To accomplish that, we shall try to prove in a logical way that certain proportions are what they are.

Most people find it quite difficult to perceive the relative proportions of the features and the skull.

In this introduction to profile-portrait drawing, I’ll concentrate on two critical relationships that are persistently difficult for beginning drawing students to correctly perceive: the location of eye level in relation to the length of the whole head; and the location of the ear in the profile view. I believe these are two examples of perceptual errors caused by the brain’s propensity to change visual information to better fit its concepts.

Let me explain. To most people, the eye level line (an imaginary horizontal line that passes through the inside corners of the eyes) appears to be about one-third of the way down from the top of the head. The actual measure is one-half. I think this misperception occurs because we tend to see that the important visual information is in the features, not in foreheads and hair areas. Apparently, the top half of the head seems less compelling than the features, and therefore is perceived as smaller. This error in perception results in what I’ve called the “chopped-off-skull error,” my term for the most common perceptual error made by beginning drawing students (Figures 9-6, 9-7).

I stumbled on this problem one day while teaching a group of beginning drawing students at the university. They were working on portrait drawings and one after another had “chopped off” the skull of the model. I went through my “Can’t you see that the eye level line is halfway between the bottom of the chin and the top edge of the hair?” queries. The students said, “No. We can’t see that.” I asked them to measure the model’s head, then their own heads, and then each others’ heads. “Was the measure one to one?” I asked. “Yes,” they said. “Well,” I said, “now you can see on the model’s head that the proportional relationship is one to one, isn’t that true?” “No,” they said, “we still can’t see it.” One student even said, “We’ll see it when we can believe it.”

This went on for a while until finally the light dawned and I said, “Are you telling me that you really can’t see that relationship?” “Yes,” they said, “we really can’t see it.” At that point I realized that brain processes were actually preventing accurate perception and causing the “chopped-off-skull” error. Once we all agreed on this phenomenon, the students were able to accept their sightings of the proportion, and soon the problem was solved.

Now we must put your own brain into a logical box (by showing it irrefutable evidence) that will help it accept your sightings of the proportions of the head.

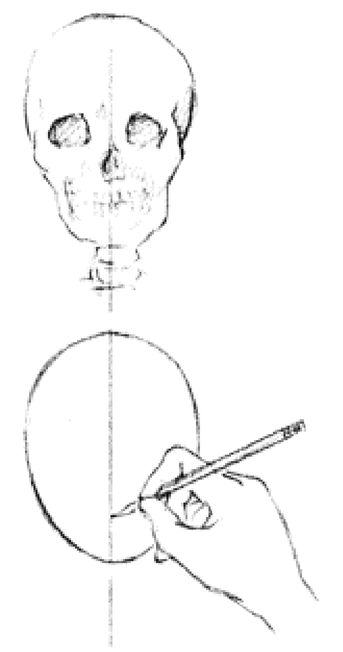
1. Draw a “blank,” an oval shape used by artists to represent the human skull in diagrams. The shape is shown in Figure 9-8. Draw a vertical line through the center of the blank, dividing the shape in half. This is called the central axis.

2. Next, you will locate the horizontal “eye level line,” which crosses the central axis at a right angle. Use your pencil to measure on your own head the distance from the inside corner of your eye to the bottom of your chin. Do this by placing the eraser end (to protect your eye) at the inside corner of your eye and marking with your thumb where your chin hits the pencil, as in Figure 9-9. Now, holding that measurement, raise the pencil, as in Figure 9-10, and compare the first distance (eye level to chin) with the distance from your eye level to the top of your head (feel across from the end of the pencil to the topmost part of your head). You will find that those two distances are approximately the same.