The New Drawing on the Right Side of the Brain (30 page)
Read The New Drawing on the Right Side of the Brain Online
Authors: Betty Edwards

BOOK: The New Drawing on the Right Side of the Brain
12.19Mb size Format: txt, pdf, ePub

Lupe Ramirez.
I
n this chapter, you will learn the third basic skill of drawing, how to see and draw relationships. You will learn how to draw “in perspective” and “in proportion.” Another term for acquiring this skill is “learning how to sight.”
n this chapter, you will learn the third basic skill of drawing, how to see and draw relationships. You will learn how to draw “in perspective” and “in proportion.” Another term for acquiring this skill is “learning how to sight.”
Learning this skill is perhaps comparable to learning the rules of grammar in reading and writing. Just as good grammar causes words and phrases to hang together logically and to communicate ideas clearly, skillful sighting of proportions and perspective causes edges, spaces, relationships, lights and shadows to come together with visual logic. Clear perception of relationships enables us to depict on a flat surface the world we see around us. Moreover, just as learning how to use grammar skillfully gives us power with words, learning how to draw in perspective and in proportion will give your drawings power through the illusion of space.
In speaking of grammar, I am referring to the mechanics of language, not the tedious naming of the parts of speech. By mechanics, I mean getting the subject and verb to agree, using the rules of word order and sentence structure, and so on. I couldn’t parse a complicated sentence today if I tried my best (which probably indicates its usefulness or lack thereof), but I’ve learned and practiced the mechanics of language for so long they are on automatic. This is what we are aiming for in this chapter: You will learn to use perspective and proportion in your drawing. You will not learn tedious and cumbersome terminology of vanishing points, converging parallel lines, and perspective of ellipses. You will learn the mechanics of sighting, which is what most artists use.
Some of my students, nevertheless, still complain that learning to sight seems so “left-brained” after the R-mode joy of drawing edges and negative spaces. Indeed, there are lots of little steps and instructions in the beginning. But almost every skill requires a component similar to sighting in drawing. For example, learning to drive a car requires that at some point you learn the rules of the road. Tedious? Yes, but without them, you are very likely to be arrested or to have an accident. Significantly, once these rules are learned and “on automatic,” you drive a car by the rules without even thinking of them.
It is the same with drawing. Once you have worked your way through the next exercise, you will have learned the “rules of the road” of drawing. With a bit of practice, sighting goes on automatic and you will hardly be aware of taking sights and comparing proportions. Best of all, you will have achieved the power to depict three-dimensional space in your drawings.
Students of drawing who learn everything except how to sight relationships greatly handicap their drawing and find themselves constantly making baffling mistakes in proportion and perspective. This problem plagues students new to drawing and, I might add, some rather advanced students as well.
Why does this skill seem so difficult? First, it is a two-part skill. The first part is sighting angles relative to vertical and horizontal, and the second part is sighting proportions relative to each other. In addition, the skill requires that one deal with ratios and comparisons that seem quite “left-brained.” And, finally, it requires that one confronts and deals with paradoxes. For example, we can know that a ceiling is flat and the corner is a right angle. But on the picture plane, the edges of the ceiling are not horizontal and the corner angles are not right angles at all. They are oblique angles. As you can imagine, we’ll have to carefully outmaneuver your L-mode, which will soon be saying, “This doesn’t make sense!” Or, “This is too complicated! I’ll never get it!” Or, “This stuff is stupid!”
On my word, learning how to sight relationships is not boring; it is powerful—it unlocks space. I agree, the skill is complicated, but you’ve learned other complicated things before this—how to read and write, for example. And sighting is definitely not stupid; it is intellectually fascinating—witness the many great thinkers of the Renaissance who grappled with the problem of how to depict space on a flat surface.
Once L-mode complaints are set aside, I believe you will actually enjoy learning this skill. I’m sure you can see the connection between learning to see and draw what is right there in front of your eyes and learning to be a more “clear-sighted” person, able to deal with contradictory information and the many paradoxes of our world. Be prepared for all of the objections. Your L-mode will have a field day, but stay with me! I’ll try to be as clear as possible.

Demonstration drawing by Grace Kennedy.

Demonstration drawing by the author.

Fig. 8-1. Roll up a tube of paper and check the relationship of sizes of a nearby object (someone’s head, for example) and a similar object farther away. You will be surprised at the apparent change in size.

Fig. 8-2. Laurie Kuroyama. Notice the great change in head size from near to far.
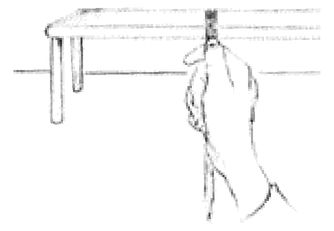
Fig. 8-3.
On dealing with the two-part skill of sighting angles and proportionsThe term sighting really means seeing, but seeing in the artist’s special way—seeing relationships on the picture plane (See Figures 8-1 and 8-2). All of sighting is comparison: What is this angle compared to vertical? How big is the apple compared to the melon? How wide is the table compared to its length? All comparisons are made relative to constants: Angles are compared to the constants vertical and horizontal. Sizes (proportions) are also compared to a constant—our Basic Unit.
On dealing with ratios: The root of the word “relationship” is ratio. In mathematics, ratios are expressed as numbers—1:2 means one of this to two of that. Ratios seem like a left-brained concept because they are strongly connected in our minds with mathematics. But we use ratios in many ordinary activities. In cooking, for example, candy is one part liquid to two parts sugar—that is, 1:2. In map reading, city X is three times as far as city Y—the ratio is 3:1. In drawing, ratios become handy tags to assess proportional relationships among the parts of a composition. The artist chooses something to be “One,” our Basic Unit, and that unit is rationalized or proportionalized with all other parts.
To illustrate, the width of a window can be called “One,” the Basic Unit. In comparison, let’s say that the window is twice as long as it is wide. The ratio is 1:2. The artist draws the width, calls it “One,” measures it as “One” and then measures off two Basic Units, counting “One to one, two.” The ratio is 1:2. It’s an easy way to tag and remember a proportion long enough to transfer it into your drawing.
On dealing with paradox: Seen flattened on the plane, a table may appear (by taking a sight) to be narrower than you know it to be (see Figure 8-3). The sighted ratio might be 1:8, for example. You must learn to “swallow” this visual paradox and draw what you have seen on the plane. Only then will the table in your drawing appear, paradoxically, to be the size and shape you know it to be. Moreover, the angles of the tabletop may appear to be different from what you know to be right angles. You must “swallow” this paradox as well.
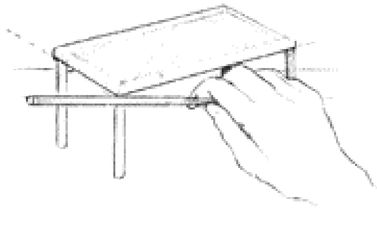
Sighting can be used to determine the relationship of lengths and widths of forms. When drawing a table viewed from an oblique angle, for example, an artist first determines angles of the edges relative to horizontal and vertical by sighting, as in Figure 8-4.
Other books
Crossroads Revisited by Keta Diablo
100% Pure Cowboy by Cathleen Galitz
Murder à la Carte by Susan Kiernan-Lewis
Incriminating Evidence by Sheldon Siegel
Prince of Fools (The Red Queen's War) by Lawrence, Mark
The Wind Between the Worlds by Lester del Rey
Charity Moon by DeAnna Kinney
While She Was Sleeping... by Isabel Sharpe
Central by Raine Thomas