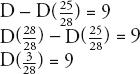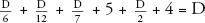Alex’s Adventures in Numberland (33 page)

Diophantus lived in Alexandria sometime between the first and the third centuries ce. Nothing else is known of his personal life except for the following riddle, which appeared in a Greek collection of puzzles and is said to have been inscribed on his tomb:

The words are perhaps less an accurate description of Diophantus’s family circumstances than they are a tribute to the man whose innovative notation presented new methods for solving problems like the one above. The ability to express mathematical sentences clearly, devoid of confusing verbiage, opened the doors to new techniques. Before I show how to solve the epitaph, let’s look at some of them.

Algebra is the generic term for the maths of equations, in which numbers and operations are written as symbols. The word itself has a curious history. In medieval Spain, barbershops displayed signs saying
Algebrista y Sangrador
. The phrase means ‘Bonesetter and Bloodletter’, two trades that used to be part of a barber’s repertoire. (This is why a barber’s pole has red and white stripes – the red symbolizes blood, and the white symbolizes the bandage.)

The root of
algebrista
is the Arabic
al-jabr
, which, in addition to referring to crude surgical techniques, also means restoration or reunion. In ninth-century Baghdad, Muhammad ibn Musa al-Khwarizmi wrote a maths primer entitled
Hisab al-jabr w’al-muqabala
, or
Calculation by Restoration and Reduction
. In it, he explains two tich, iques for solving arithmetical problems. Al-Khwarizmi wrote out his problems rhetorically, but here, for ease of understanding, they are expressed in modern symbols and terminology.

Consider the equation A = B – C.

Al-Khwarizmi described
al-jabr
, or restoration, as the process by which the equation becomes A + C = B. In other words, a negative term can be made positive by resetting it on the other side of the equal sign.

Now, consider the equation A = B + C.

Reduction is the process that turns the equation into A – C = B.

Thanks to modern notation, we can now see that both restoration and reduction are examples of the general rule that
whatever
you do to one side in an equation, you must do to the other as well. In the first equation we
added
C to both sides. In the second equation we
subtracted
C from both sides. Because by definition the expressions on either side of an equation are equal, they must continue to be equal when another term is simultaneously added to or subtracted from either side. It follows that if we multiply one side by an amount, we must multiply the other by the same amount, and the same applies for division and other operations.

The equals sign is like a picket fence separating the gardens of two very competitive families. Whatever the Joneses do to their garden, the Smiths next door will do exactly the same.

Al-Khwarizmi wasn’t the first person to use restoration and reduction – these operations could also be found in Diophantus; but when Al-Khwarizmi’s book was translated into Latin, the
al-jabr
in the title became
algebra
. Al-Khwarizmi’s algebra book, together with another one he wrote on the Indian decimal system, became so widespread in Europe that his name was immortalized as a scientific term: Al-Khwarizmi became Alchoarismi, Algorismi and, eventually, algorithm.

Between the fifteenth and seventeenth centuries mathematical sentences moved from rhetorical to symbolic expression. Slowly, words were replaced with letters. Diophantus might have started letter symbolism with his introduction of
for the unknown quantity, but the first person to effectively popularize the habit was François Viète in sixteenth-century France. Viète suggested that upper-case vowels – A, E, I, O, U – and Y be used for unknown quantities, and that the consonants B, C, D, etc., be used for known quantities.

Within a few decades of Viète’s death, René Descartes published his
Discourse on Method
. In it, he applied mathematical reasoning to human thought. He started by doubting all of his beliefs and, after stripping everything away, was left with only certainty that he existed. The argument that one cannot doubt one’s own existence, since the process of thinking requires the existence of a thinker, was summed up in the
Discourse
as
I think, therefore I am
. The statement is one of the most famous quotations of all time, and the book is considered a cornerstone of Western philosophy. Descartes had originally intended it as an introduction to three appendices of his other scientific works. One of them,
La Géométrie
, was equally a landmark in the history of maths.

In
La Géométrie
Descartes introduces what has become standard algebraic notation. It is the first book that looks like a modern maths book, full of
a
s,
b
s and
c
s and
x
s,
y
s and
z
s. It was Descartes’s decision to use lower-case letters from the beginning of the alphabet for known quantities, and lower-case letters from the end of the alphabet for the unknowns. When the book was being printed, however, the printer started to run out of letters. He enquired if it mattered if
x
,
y
or
z
was used. Descartes replied not, so the printer chose to concentrate on
x
since it is used less frequently in French than
y
or
z
. As a result,
x
became fixed in maths – and the wider culture – as the symbol for the unknown quantity. That is why paranormal happenings are classified in the X-Files and why Wilhelm Röntgen came up with the term X-ray.

Were it not for issues of limited printing stock, the Y-factor could have become a phrase to describe intangible star quality and the African-American political leader might have gone by the name Malcolm Z.

With Descartes’ symbology, all traces of rhetorical expression had been expunged.

Replacing words with letters and symbols was more than convenient shorthand. The symbol
x
may have started as an abbreviation for ‘unknown quantity’, but once invented, it became a powerful tool for thought. A word or an abbreviation cannot be subjected to mathematical operations in the way that a symbol such as
x
can. Numbers made counting possible, but letter symbols took mathematics into a domain far beyond language.

When problems were expressed rhetorically, as in Egypt, mathematicians used ingenious, but rather haphazard, methods to solve them. These early problem-solvers were like explorers stuck in a fog with few tricks to help them move about. When a problem was expressed using symbols, however, it was as though the fog lifted to reveal a precisely defined world.

The marvel of algebra is that once a problem is restated in symbolic terms, often it is almost solved.

For example, let’s re-examine Diaphantus’s epitaph. How old was he when he died? Translating that statement, using the letter D to symbolize his age when he died, the epitaph says that for D—6 years he was a boy, that another D—12 years passed before he sprouted facial hair, and that he wed after another D—7. Five years after that he had a son, who lived for D—2 years, and four years later Diophant us himself breathed his last. The sum of all these time intervals adds up to D, since D is the number of years Diophantus lived. So:

The lowest common denominator of the fractions is 84, so this becomes:

Which can be rearranged as:

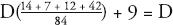
Or:

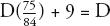
Which is:

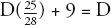
Moving the Ds to the same side: