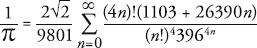Alex’s Adventures in Numberland (29 page)

Probability of the needle touching the line =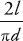

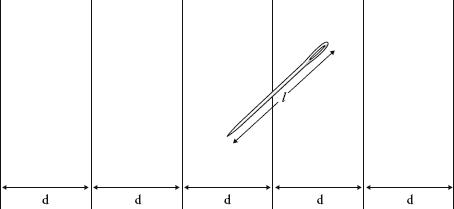
A few years after Buffon died, Pierre Simon Laplace realized that this equation could be used to estimate a value for pi. If you throw lots and lots of needles on the floor, then the ratio of the number of times that the needle hits the line to the total number of throws will be approximately equal to the mathematical probability of the needle touching the line. In other words, after many throws

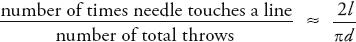
or:

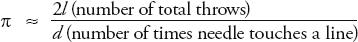
(The symbol
means ‘is approximately equal to’.)

Even though Laplace was the first to write about how pi could be estimated this way, his work followed from Buffon’s equation, so Buffon is the person remembered for it. His achievement put him in esteemed company as a member of the club of mathematicians, including Archimedes and Leibniz, who each found a new way to calculate pi.

The more throws of the needle that are taken, the better the approximation, and aiming needles at boards has become a standard diversion for mathematicians unable to think of more creative ways to pass the time. You need, however, to keep on going a fair while before any interesting result is achieved. An early adopter is said to have been a certain Captain Fox in the American Civil War, who, while recovering from battle wounds, threw a piece of wire eleven hundred times on a board of parallel lines and managed to derive pi to 2 decimal places.

Pi’s mathematical properties have made it a celebrity among numbers, and also a more general cultural icon. Because pi’s digits never repeat, they are perfect for feats of memorization. If remembering numbers is your thing, the
ne plus ultra
of digits is the digits in pi. This has been a pastime since at least 1838, when
The Scotsman
reported that a 12-year-old Dutch boy recited all the 155 digits that were known at the time to an audience of scientists and royals. Akira Haraguchi, a 60-year-old retired engineer, holds the current world record. In 2006 he was filmed in a public hall near Tokyo reciting pi to 100,000 decimal places. The performance took him 16 hours and 28 minutes, including five-minute breaks every two hours to eat rice balls. He explained to a journalist that pi symbolized life since its digits never repeated and followed no pattern. Memorizing pi, he added, was ‘the religion of the universe’.

Pi memorization gets a little dull, but pi memorization while juggling, now there’s a competitive sport! The record is held by Mats Bergsten, an actuary in Sweden in his late fifties, who has recited 9778 digits while juggling with three balls. He told me, however, that he is proudest of his achievements in the ‘erest test’, in which the first 10,000 digits of pi’s expansion are divided into 2000 groups of five, beginning with 14159. In the test 50 groups are randomly read out, and the contestant has to say from memory which five numbers precede and succeed each of them. Mats Bergsten is one of only four people in the world who can do this with no errors, and his time, 17min 39secs, is the fastest. It is much more mentally straining, he told me, to recall 10,000 digits randomly than merely remembering them in order.

When Akira Haraguchi recited 100,000 digits of pi by heart, he used a mnemonic technique, assigning syllables to each number from 0 to 9 and then translating pi’s decimals into words, which in turn formed sentences. The first fifteen digits sounded like: ‘the wife and children have gone abroad; the husband is not scared.’ Using words to remember the digits in pi this way is used by schoolchildren in cultures all over the world, but usually this is done not by assigning syllables, but by creating a phrase in which the number of letters in each word represents each consecutive digit in the decimal expansion of pi. A well-known English one is credited to the astrophysicist Sir James Jeans:
How I need a drink, alcoholic in nature, after the heavy lectures involving quantum mechanics. All of thy geometry, Herr Planck, is fairly hard
. ‘How’ has 3 letters, ‘I’ has 1, ‘need’ has 4, and so on.

Among numbers, only pi has inspired this type of fandom. No one wants to memorize the square root of two, which is just as challenging. Pi is also the only number to have inspired its own literary subgenre. Constrained writing is a technique in which some condition is adopted that imposes a pattern or forbids certain things in the text. Entire poems – or ‘piems’ – have been written under the constraint that the number of letters per word is determined by pi, usually with the convention that a 0 in the expansion requires a ten-letter word. The most ambitious piem is the
Cadaeic Cadenza
by Mike Keith, which follows pi for 3835 digits. It begins as a pastiche of Edgar Allan Poe:

Keith says that writing with a difficult constraint is an exercise both in discipline and discovery. Since the digits in pi are random, the constraint is, he said, ‘like bringing order out of chaos’. When I asked him ‘Why pi?’ he replied that pi was ‘a metaphor for all things infinite, or inscrutable, or unpredictable, or full of endless wonder’.

Pi has gone by this name only since 1706, when the Welshman William Jones introduced the symbol p in his book, the snappily titled
A New Introduction to the Mathematics, for the Use of some Friends who have neither Leisure, Convenience, nor, perhaps, Patience, to search into so many different Authors, and turn over so many tedious Volumes, as is unavoidably required to make but tolerable progress in the Mathematics
. The Greek letter, which was probably an abbreviation for the word periphery, did not immediately catch on, howeve, becoming standard notation for pi only 30 years later when Leonhard Euler adopted it.

Euler was the most prolific mathematician of all time (he published 886 books), and he is possibly the one who contributed most to an understanding of pi. It was his improved formulae for pi that enabled the eighteenth-and nineteenth-century digit-hunters to peel back more and more decimal places. In the beginning of the twentieth century the Indian mathematician Srinivasa Ramanujan devised many more Euler-style infinite series for pi.

Ramanujan was a largely self-taught mathematician who worked as a clerk in Madras before writing a letter to Cambridge university professor G.H. Hardy. Hardy was flabbergasted to see that Ramanujan had rediscovered results that had taken centuries to achieve, and invited him to England, where the men collaborated before Ramanujan died aged 32. His work showed an extraordinary intuition about the properties of numbers, including pi, and his most famous formula is the following:

The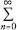
symbol indicates a series of values all added up, starting with the value when
n
equals zero, added to the value when
n
equals one, and so on to infinity. Even without understanding the notation, however, one can appreciate the drama of such an equation. The Ramanujan formula races towards pi with remarkable speed. From the very start, when
n
is 0 the formula has one term and gives a value of pi accurate to six decimal places. For each increase in the value of
n
, the formula adds roughly eight new digits to pi. It is an industrial-strength pi-making machine.