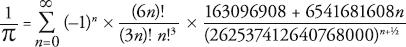Alex’s Adventures in Numberland (30 page)

Inspired by Ramanujan, in the 1980s the Ukrainian-born mathematicians Gregory and David Chudnovsky devised an even more ferocious formula. Each new term adds roughly 15 digits.

The first time I saw the Chudnovsky formula I was standing on it. Gregory and David are brothers and they share an office at the Polytechnic University in Brooklyn. It consists of an open-plan space with a sofa in the corner, a couple of chairs and a blue floor decorated with dozens of formulae for pi. ‘We wanted to put something on the floor and what else can you put on the floor other than stuff which relates to mathematics?’ explained Gregory.

In fact, the pi floor pattern was their second choice. The original plan was to lay down a giant reproduction of
Melencolia I
by Albrecht Dürer (reproduced on chapter 6). The sixteenth-century woodcut is beloved of mathematicians since it is full of playful references to numbers, geometry and perspective.

‘One night, when there was nothing on the surface, we printed 2000 or more pages of [
Melencolia I
] and we laid it on the floor,’ said David. ‘But if you walked around it, you wanted to throw up! Because your point of view changes extremely abruptly.’ David began to study the floors of the cathedrals and castles of Europe in order to work out how he could decorate the office without inducing nausea in anyone walking through. ‘I discovered they are mostly laid out in a –’

‘Simple geometric style,’ interrupted Gregory.

‘Black, white, black, white squares…#8217; said David.

‘You see, if you really have a complex picture and you try to walk on it, the angle changes so abruptly that your eyes don’t like it,’ added Gregory. ‘So the only way you can do something like that is to –’

‘Hang from the ceiling!’ David shouted in my left ear, and both men lost themselves in guffaws.

Talking to the Chudnovskys was like wearing stereo headphones with an erratically alternating connection to both ears. They sat me on their sofa and sat on either side of me. Constantly interrupting each other, they finished each other’s sentences, speaking in a highly melodic English thick with Slavic tones. The brothers were born in Kiev, when it was in the Soviet Republic of Ukraine, although they have lived in the United States since the late 1970s and are American citizens. They have collaborated on so many papers and books together that they encourage you to think of them as one mathematician, not two.

For all their genetic, conversational and professional homogeneity, however, the men look very different. This is mostly because Gregory, who is 56, suffers from
myasthenia gravis
, an auto-immune disorder of the muscles. He is so thin and frail that he spends most of his time lying down. I never saw him get up off the sofa. Still, the energy his limbs lacked was compensated for by a brilliantly expressive face that burst into life as soon as he talked about maths. He has pointed features, large brown eyes, a white beard and wispy unkempt hair. David, who has blue eyes, is five years older, rounder of body and fuller of face. He was clean-shaven and his short hair was hidden under an olive-green baseball cap.

The Chudnovskys are arguably the mathematicians who have done the most to popularize pi in recent years. In the early 1990s they built a supercomputer in Gregory’s Manhattan apartment out of mail-order parts that, using their own formula, calculated the number to more than two billion decimal places – a record at the time.

This amazing achievement was chronicled in a
New Yorker
article, which in turn inspired the 1998 film
Pi
. The main protagonist was an unruly-haired maths genius looking for hidden patterns in stock-market data on a homemade supercomputer. I was curious to discover if the Chudnovskys had seen the film, which garnered favourable reviews and has become a reference for low-budget, black-and-white psycho-mathematical thrillers. ‘No, no, we haven’t seen it,’ said Gregory.

‘You have to realize, usually movie-makers repeat their internal state,’ added David sarcastically.

I tell them I thought they might have been flattered by the attention.

‘No, no,’ grinned Gregory.

‘Let me tell you another thing,’ David cut in. ‘Two years ago I came back from France. A couple of days before I left, there was a huge book fair. I stopped at a stand where there was a book that had a detective story on it. It was written by an engineer. It was a murder mystery, you know. A lot of dead bodies, mostly mistress in hotel, and the source that determined everything he did was pi.’

Gregory was smiling from ear to ear and said under his breath: ‘OK, I am not going to read this book,
zat’s
for sure.’

David carried on: ‘So I talked to the guy. He is a very eucated man.’ He paused, shrugged his shoulders and raised his pitch by an octave: ‘As I say, I bear no responsibility!’

David said that he was taken aback the first time that he saw billboards advertising the Givenchy perfume. ‘All the way down the street was pi…pi…pi…’ He was wailing now: ‘
Pi…pi…pi!
Do I bear any responsibility?’

Gregory glanced at me and said: ‘For some reason, the general public is fascinated with this stuff. They get kind of the wrong inference.’ There are many professional mathematicians, he said, who study pi. He added wryly: ‘Usually these people are not allowed to see the light of day.’

In the 1950s and 1960s advances in computer technology were reflected in the number of new digits found in pi. By the end of the 1970s the record had been broken nine times and stood at just over a million decimal places. In the 1980s, however, a combination of even faster computers and brand-new algorithms led to a frenetic new era of digit-hunting. Yasumasa Kanada, a young computer scientist at Tokyo University, was first off the block in what became a two-way pi race between Japan and the United States. In 1981 he used an NEC computer to calculate pi to 2 million digits in 137 hours. Three years later he was up to 16 million. William Gosper, a mathematician in California, then nudged into the lead with 17.5 million, before David H. Bailey, at NASA, bettered him with 29 million. In 1986 Kanada overtook them both with 33 million and broke his own record three times in the next two years to reach 201 million with a new machine, the S-820, which did the calculation in just under six hours.

Away from the digit-hunting spotlight, the Chudnovskys were also beavering away on pi. Using a new method of communication called the internet, Gregory connected the computer at his bedside to two IBM supercomputers at different sites in the US. The brothers then devised a program to calculate pi based on the new superfast pi formula they had discovered. They were allowed on to the computers only when no one else was using them, at nights and weekends.

‘It was a great thing,’ remembered Gregory nostalgically. In those days there was no computer capacity to store the numbers that the brothers were calculating. ‘They kept the pi on magnetic tape,’ he said.

‘Mini-tape. And you had to call the guy and ask…’ added David.

‘And say tape number such and such,’ continued Gregory. ‘And sometimes if somebody else is more important your tapes are dismounted in the middle of computation.’ His eyes rolled as if to throw his hands in the air.

Despite the obstacles, the Chudnovskys kept on going, pushing beyond a billion digits. Kanada then nudged ahead of them briefly, before the Chudnovskys retook the lead with 1.13 billion. David and Gregory then decided that if they were serious about calculating pi they needed their own machine.

The Chudnovskian supercomputer lived in a room in Gregory’s apartment. Made up of processors linked by cables, the whole thing cost, according to their estimates, about $70,000. It was a steal, compared to the millions of dollars that would have bought a machine of similar capacity; although it came with its own complications to their lifestyles. The computer, which they called
m zero
, was switched on at all times, just in case switching it off was irreversible, and keeded 25 fans in the room to keep it cool. The brothers were careful not to switch on too many lights in the apartment just in case the added demand blew the wiring.

In 1991 David and Gregory’s homemade contraption calculated pi to more than two billion places. Then they got distracted by other problems. By 1995 Kanada was ahead once again, and he reached 1.2 trillion digits in 2002, a record that lasted only until 2008, when compatriots at the University of Tsukuba revealed 2.6 trillion. In December 2009 the Frenchman Fabrice Bellard claimed a new record using the Chudnovsky formula: almost 2.7 trillion places. The calculation had taken 131 days on his desktop PC.

If you wrote a trillion digits in small type, the distance would cover from here to the sun. If you put 5000 digits on a page (which is very small type) and stacked the pages on top of each other, the pi in the sky would be 10km high. What is the point of calculating pi to such absurd lengths? One reason is very human: records exist to be broken.

But there is another, more important motivation. Finding new digits in pi is ideal for testing the processing capacity and reliability of computers. ‘I have no interest as a hobby for extending the known value of pi itself,’ Kanada once said. ‘I have a major interest for improving the performance of the computation.’ Pi calculation is now essential for quality-testing supercomputers because it is a ‘high-duty job which requires large main memory, operates huge number-crunching and gives [an] easy [way] to check [the] correct answer. Mathematical constants like the square root of two,
e
^*
[and] gamma are some of the candidates, but pi is most effective.’

The story of pi has wonderful circularity. It is the simplest and most ancient ratio in maths, which has been reinvented as a massively important tool on the frontline of computer technology.

In fact, the Chudnovskys’ interest in pi came primarily from their desire to build supercomputers, a passion that still burns brightly. The brothers are currently designing a chip that they claim will be the fastest in the world, only 2.7cm wide but containing 160,000 smaller chips and 1.75km of wire.

On discussion of their new chip, Gregory became very high-spirited: ‘Computers double their power every 18 months, not because they are faster but because they can pack more stuff in. But there is a catch,’ he said. The mathematical challenge was how to partition the smaller pieces so that they can talk to each other in the most efficient way. His laptop showed the chip’s circuitry. ‘I’d say the problem with this chip is that it is a capitalist chip!’ he exclaimed. ‘The problem is that most of the stuff here is not doing anything. There are not too much proles here.’ He pointed at one section. ‘This is just management of the stores inside the chip,’ he lamented. ‘The majority of these guys just do warehousing and accounting. This is awful! Where is the manufacturing sector?’

In Carl Sagan’s bestselling book
Contact
, an extraterrestrial informs a woman on Earth that after a certain amount of digits the randomness in pi stops and there is a message written in 0s and 1s. This message occurs after 10
²⁰
decimal places – which is the number described by 1 followed by 20 zeros. Since we currently know pi to ‘only’ 2.7 trillion places (27 followed by 11 zeros), we have a little way to goe s to check that he was making it up. Actually, we have further to go since the message is apparently written in base 11.

The idea that there is a pattern in pi is an exhilarating one. Mathematicians have been looking for signs of order in the decimal expansion of pi for as long as there have been decimal expansions. The irrationality of pi means that the numbers keep on spewing out with no repeated pattern, but this does not eliminate the possibility of patches of order – such as a message written in 0s and 1s. So far, however, no one has found anything significant. The number, does, though, have its quirks. The first 0 comes in position 32, which is much later than expected if the digits are randomly distributed. The first time a digit is repeated six times consecutively is 999999 at the 762nd decimal place. The likelihood of six 9s occurring so early if they occur randomly is less than 0.1 percent. This sequence is known as the Feynman point, since physicist Richard Feynman once remarked that he wanted to memorize pi until that point and finish by saying ‘nine, nine, nine, nine, nine, nine, and so on’. The next time pi throws up six consecutive identical digits happens in position 193,034 and they are also 9s. Is this a message from beyond, and if so what is it saying?

A number is considered
normal
if each of the digits 0 to 9 occurs equally often in the number’s decimal expansion. Is pi normal? Kanada looked at the first 200 billion digits of pi and found that the digits occurred with the following frequencies: