Alex’s Adventures in Numberland (28 page)
Read Alex’s Adventures in Numberland Online
Authors: Alex Bellos

To square a circle we must construct (using just a compass and straightedge) a square that has the same area as a given circle. Now we know that a line with length
r
is the radius of a circle with area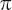 r
r
2
, and we also know that a square with area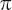 r
r
2
must have a side length
r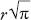 (since (
(since (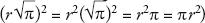 ). So squaring the circle can be reduced to the challenge of constructing the length
). So squaring the circle can be reduced to the challenge of constructing the length
r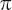 from the length
from the length
r
. Or, taking
r
as 1 for convenience, the length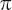 from 1.
from 1.
Using coordinate geometry, which I will cover later, it is possible to express the process of the construction of a line algebraically, as a finite equation. It can be shown that so long as
x
is the solution to a finite equation, then starting with a line of length 1 we can construct a line with length
x
. But if
x
is not the solution to a finite equation – in other words, if
x
is transcendental – it is impossible to construct a line with length
x
. Now, the fact that p is transcendental means that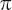 is also transcendental. (You’re going to have to trust me on that.) So it is impossible to construct the length
is also transcendental. (You’re going to have to trust me on that.) So it is impossible to construct the length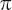 . The transcendence of pi proves that the circle cannot be squared.
. The transcendence of pi proves that the circle cannot be squared.
Lindemann’s proof of the transcendence of pi dashed what had been the dream, for thousands of years, of countless mathematicians. Perhaps the most eminent figure ever to have declared that he had squared the circle was Thomas Hobbes, the seventeenth-century English thinker whose book
Leviathan
founded political philosophy. Having become a keen amateur geometer in later life, Hobbes published his solution when he was 67. Even though circle-squaring was still an open question at the time, his proof was received with bemusement by the scientific community. John Wallis, professor at Oxford and the finest British mathematician before Isaac Newton, exposed Hobbes’s errors in a pamphlet, thus setting in motion one of the most entertaining – and pointless – feuds in the history of British intellectual life. Hobbes replied to Wallis’s comments with an addendum to his book entitled
Six Lessons to the Professors of Mathematics
. Wallis countered with
Due Correction for Mr Hobbes in School Discipline for not saying his Lessons right
. Hobbes followed this with
Marks of the Absurd Geometry, Rural Language, Scottish Church Politics and Barbarisms of John Wallis
. This led to Wallis’s
Hobbiani Puncti Dispunctio! or the Undoing of Mr Hobbes’s Points
. The quarrelling lasted almost a quarter of a century, until Hobbes’s death in 1679. Wallis rather enjoyed the hostilities, since it was a way of casting aspersions on Hobbes’s political and religious views, which he despised. And, of course, he was right. In many disputes truths are shared between both sides. Not in Hobbes vs Wallis. Hobbes could not square the circle because it is impossible to do so.
Proof that you cannot square the circle has not put people off trying. In 1897 the Indiana state legislature famously considered a bill containing a proof of squaring the circle by E.J. Goodwin, a country doctor, who offered it ‘as a gift to the State of Indiana’. He was, of course, misguided. Since Ferdinand von Lindemann in 1882, the phrase circle-squarer has been mathspeak for crank.
Pi’s enigmatic attributes were, in the eighteenth and nineteenth centuries, revealed not only to be at the heart of ancient geometrical problems but also deeply rooted in new fields of science that were not always obviously related to circles. ‘This mysterious 3.141592…which comes in at every door and window, and down every chimney,’ wrote the British mathematician Augustus De Morgan. For example, the time it takes a pendulum to swing is dependent on pi. The distribution of deaths in a population is a function of pi. If you toss a coin 2
n
times, the probability when
n
is very large of getting exactly 50 percent heads and 50 percent tails is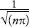 .
.
The man whose name is most associated with offbeat occurrences of pi was the French polymath Georges-Louis Leclerc, the Comte de Buffon (1707–88). Of Buffon’s many colourful scientific endeavours, perhaps his most ambitious was the construction of a working version of Archimedes’ weapon of mirrors, with which he was said to have set fire to ships. Buffon’s contraption was made up of 168 flat mirrors, each six by eight inches, and it was able to ignite a wooden plank at a distance of 150 feet, a good effort, though on a different scale from setting a Roman fleet ablaze.
With regard to pi, Buffon is remembered for having devised an equation that led to a new method for calculating pi, though Buffon did not himself make the connection. Buffon arrived at his equation by studying an eighteenth-century gambling game called ‘clean tile’, in which you throw a coin on to a tiled surface and bet on whether it will touch the cracks between tiles or rest cleanly. Buffon came up with the following alternative scenario: imagine that a floor is marked with parallel lines spaced evenly apart and that a needle is thrown on it. He then correctly calculated that if the length of the needle is
l
and the distance between lines is
d
, then the following equation holds: