Alex’s Adventures in Numberland (56 page)

De Méré’s second question, about divvying up the pot, is often called the
problem of points
and had been posed before Fermat and Pascal tackled it, but never correctly resolved. Let’s restate the question in terms of heads and tails. Jean wins each round if the coin lands on heads, and Jacques wins if it lands on tails. The first person to win three rounds takes the pot of 64. With the score at two heads for Jean and one tails for Jacques, the game needs to come to an abrupttop. If this is the case, what’s the fairest way to divide the pot? One answer is that Jean should take the lot, since he is ahead, but this doesn’t take account of the fact that Jacques still has a chance of winning. Another answer is that Jean should take twice as much as Jacques, but again this is not fair because the 2–1 score reflects past events. It’s not an indication of what might happen in the future. Jean is not better at guessing coins than Jacques. Each time they throw, there is a 50:50 chance of the coin landing heads or tails. The best, and fairest, analysis is to consider what might happen in the future. If the coin is tossed another two times, the possible outcomes are:

After these two throws, the game has been won. In the first three instances Jean wins, and in the fourth Jacques does. The fairest way to divide the pot is for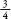
to go to Jean and
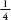to go to Jacques, so the cash is divided 48 francs to 16. This seems fairly straightforward now, but in the seventeenth century the idea that random events that haven’t yet taken place can be treated mathematically was a momentous conceptual breakthrough. The concept underpins our scientific understanding of much of the modern world, from physics to finance and from medicine to market research.

A few months after he first wrote to Fermat about the gambler’s queries, Pascal had a religious experience so intense that he scribbled a report of his trance on a piece of paper that he carried with him in a special pouch sewn into the lining of his jacket for the rest of his life. Perhaps the cause was the near-death accident in which his coach hung perilously off a bridge after the horses plunged over the parapet, or perhaps it was a moral reaction to the decadence of the dicing tables of pre-revolutionary France – in any case, it revitalized his commitment to Jansenism, a strict Catholic cult, and he abandoned maths for theology and philosophy.

Nonetheless, Pascal could not help but think mathematically. His most famous contribution to philosophy – an argument about whether or not one should believe in God – was a continuation of the new approach to analysing chance that he had first discussed with Fermat.

In simple terms,
expected value
is what you can expect to get out of a bet. For example, what could Chevalier de Méré expect to win by betting £10 on getting a six when rolling four dice? Imagine that he wins £10 if there is a six and loses everything if there is no six. We know that the chance of winning this bet is 0.518. So, just over half the time he wins £10, and just under half he loses £10. The expected value is calculated by multiplying the probability of each outcome with the value of each outcome, and then adding them up. In this case he can expect to win:

or

(In this equation, money won is a positive number, and money lost is a negative number.) Of course, in no single bet will de Méré win 36p – either he wins £10 or he loses £10. The value of 36p is theoretical, but, on average, if he keeps on betting, his winnings will approximate 36p per bet.

Pascal was one of the first thinkers to exploit the idea of expected value. His mind, though, was occupied by much higher thoughts than the financial benefits of the dicing table. He wanted to know whether it was worth placing a wager on the existence of God.

Imagine, Pascal wrote, gambling on God’s existence. According to Pascal, the expected value of such a wager can be calculated by the following equation:

So, say the chances of God existing are 50:50; that is, the probability of God’s existence is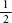
. If you believe in God, what can you expect to get out of this bet? The formula becomes:

In other words, betting on God’s existence is a very good bet because the reward is so fantastic. The arithmetic works out because half of nothing is nothing, but half of something infinite is
also
infinite. Likewise, if the chance of God existing is only a hundredth, the formula is:

Again, the rewards of believing that God exists are equally phenomenal, since one hundredth of something infinite is still infinite. It follows that, however minuscule the chance of God existing, provided that chance is not zero, if you believe in God, the gamble of believing will bring an infinite return. We have come down a complicated route and reached a very obvious conclusion. Of course Christians will gamble that God exists.

Pascal was more concerned with what happens if one doesn’t believe in God. In such cases, is it a good gamble to bet on whether God exists? If we assume the chance of God not existing is 50:50, the equation now becomes: