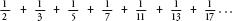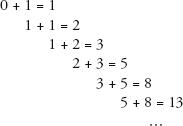Alex’s Adventures in Numberland (51 page)

adds up to infinity. Even though it starts with a tiny number and the terms get only tinier, the sum of the terms will eventually surpass any number you want. The reason, again, is because once numbers get very large, almost every number has a 314159 in it. Almost all unit fractions contain a 314159.

Let’s take a look at one last infinite series, one that brings us back to the mysteries of the primes. The prime harmonic series is the series of unit fractions where the denominators are the prime numbers:

The primes get scarcer as numbers get higher, so one might expect that this series doesn’t have the momentum to add up to infinity. Yet, unbelievably, it does. Counter-intuitive and spectacular, the result makes us realize the power and importance of the primes. They can be seen not only as the building blocks of natural numbers, but also as the building blocks of infinity.

Sitting with me in nunge at home, Eddy Levin handed me a sheet of white paper and asked me to write out my name in capital letters. Levin, who is 75 years old and has a donnish face with grey stubble and a long forehead, used to be a dentist. He lives in East Finchley, north London, on a street that is the epitome of prosperous and conservative suburban Britain. Expensive cars sat in the driveways of between-the-wars brick houses with freshly trimmed hedges and bright green lawns. I took the paper and wrote: ALEX BELLOS.

Levin then picked up a stainless-steel instrument that looked like a small claw, with three prongs. With a steady hand he held it up to the paper and started to analyse my script. He lined up the instrument to the E in my first name with the concentration of a rabbi preparing a circumcision.

‘Pretty good,’ he said.

Levin’s claw is his own invention. The three prongs are positioned in such a way that the tips of the prongs stay on the same line and in the same ratio to each other when the claw opens out. He designed the instrument so that the distance between the middle prong and the prong above it is always 1.618 times the distance between the middle prong and the prong below it. Because this number is better known as the golden mean he calls his tool the Golden Mean Gauge. (Other synonyms for 1.618 include the golden ratio, the divine proportion and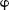
, or phi.) Levin put the gauge on my letter E so that the tip of one claw was on the top horizontal bar of the E, the middle tip was on the middle bar of the E and the bottom tip was on the bottom bar. I had assumed that when I wrote a capital E I positioned the middle bar equidistant between the top and the bottom, but Levin’s gauge showed that I was subconsciously placing the bar slightly above halfway – in such a way that it divided the height of the letter into two sections with lengths of ratio 1 to 1.618. Although I had scribbled my name with gay abandon, I had adhered to the golden mean with uncanny precision.

Levin smiled and moved on to my S. He readjusted the gauge so that the side points touched the topmost and bottommost tips of the letter and, to my further amazement, the middle one coincided exactly with the S line as it curved.

‘Spot on,’ Levin said calmly. ‘Everybody’s handwriting is in the golden proportion.’

The golden mean is the number that describes the precise ratio when a line is cut into two sections in such a way that the proportion of the entire line to the larger section is equal to the proportion of the larger section to the smaller section. In other words, when the ratio of A + B to A is equal to the ratio of A to B:

A line divided into two by the golden ratio is known as a golden section, and phi, the ratio between larger and smaller sections, can be calculated as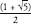
. This is an irrational number, whose decimal expansion begins:

The Greeks were fascinated by phi. They discovered it in the five-pointed star, or pentagram, which was a revered symbol of the Pythagorean Brotherhood. Euclid called it the ‘extreme and mean ratio’ and he provided a method to construct it with compass and straightedge. Since at least the Renaissancehe number has intrigued artists as well as mathematicians. The major work on the golden ratio was Luca Pacioli’s
The Divine Proportion
in 1509, which listed the appearance of the number in many geometric constructions, and was illustrated by Leonardo da Vinci. Pacioli concluded that the ratio was a message from God, a source of secret knowledge about the inner beauty of things.

Mathematical interest in phi comes from how it is related to the most famous sequence in maths: the Fibonacci sequence, which is the sequence that starts with 0, 1 and each subsequent term is the sum of the two previous terms:

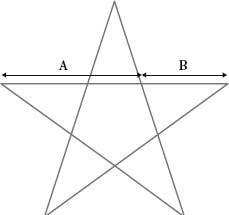
The pentagram, a mystical symbol since ancient times, contains the golden ratio.

Here is how the numbers are found:

Before I show how phi and Fibonacci are connected, let’s investigate the numbers in the sequence. The natural world has a predilection for Fibonacci numbers. If you look in the garden, you will discover that for most flowers the number of petals is a Fibonacci number:

The flowers may not always have these numbers of petals, but the average number of petals will be a Fibonacci number. For example, there are usually three leaves on a stem of clover, a Fibonacci number. Only seldom do clovers have four leaves, which is why we consider them special. Four-leaf clovers are rare because 4 is not a Fibonacci number.

Fibonacci numbers also occur in the spiral arrangements on the surfaces of pine cones, pineapples, cauliflower and sunflowers. As the picture below shows, you can count spirals clockwise and anticlockwise. The numbers of spirals you can count in both directions are consecutive Fibonacci numbers. Pineapples usually have 5 and 8 spirals, or 8 and 13 spirals. Spruce cones tend to have 8 and 13 spirals. Sunflowers can have 21 and 34, or 34 and 55 spirals – although examples as high as 144 and 233 have been found. The more seeds there are, the higher up the sequnce the spirals will go.

The Fibonacci sequence is so called because the terms appear in Fibonacci’s
Liber Abaci
, in a problem about rabbits. The sequence only gained the name, however, more than 600 years after the book was published when, in 1877, the number theorist Edouard Lucas was studying it, and he decided to pay tribute to Fibonacci by naming the sequence after him.

A sunflower with 34 anticlockwise and 21 clockwise spirals.

The
Liber Abaci
set up the sequence like this: say that you have a pair of rabbits, and after one month the pair gives birth to another pair. If every adult pair of rabbits gives birth to a pair of baby rabbits every month, and it takes one month for the baby rabbits to become adults, how many rabbits are produced from the first pair in a year?

The answer is found by counting rabbits month by month. In the first month, there is just one pair. In the second there are two, as the original pair have given birth to a pair. In the third month there are three, since the original pair have again bred, but the first pair are only just adults. In the fourth month the two adult pairs breed, adding two to the population of three. The Fibonacci sequence is the month-on-month total of pairs:

An important feature of the Fibonacci sequence is that it is
recurrent
, which means that each new term is generated by the values of previous terms. This helps explain why the Fibonacci numbers are so prevalent in natural systems. Many life forms grow by a process of recurrence.