Alex’s Adventures in Numberland (48 page)

or

This can be generalized according to the formula: 2
⁰
+ 2
¹
+ 2
²
+…+ 2
^n–1
= 2
ⁿ
– 1, in other words that the sum of the first
n
terms of the doubling sequence starting at 1 is equal to 2
ⁿ
– 1.

So, using Euclid’s original declaration that ‘whenever the sum of doubles is a prime number, the product of the sum multiplied by the highest double is a perfect number’, and adding modern algebraic notation, we can arrive at the much more concise statement:

For civilizations that prized perfect numbers, Euclid’s proof was terrific news. If perfect numbers could be generated whenever 2
ⁿ
– 1 was prime, all that needed to be done in order to find new perfect numbers was to find new primes that were written 2
ⁿ
– 1. The hunt for perfect numbers was reduced to the hunt for a certain type of prime.

Mathematical interest in prime numbers written 2
ⁿ
– 1 might have originated because of their link to perfect numbers, but by the seventeenth century the primes had became objects of fascination in their own right. In the same way that some mathematicians were obsessed with finding pi to more and more decimal places, others were preoccupied with finding higher and higher primes. The activities are similar but opposite: whereas finding digits in pi is about trying to see smaller and smaller objects, pursuing primes is about reaching towards the sky. They are missions that have been undertaken as much for the romance of the journey, as for the possible uses of the numbers discovered along the way.

In the quest for primes, the ‘2
ⁿ
– 1’ generating method took on a life of its own. It wan’t going to produce primes for every value of
n
, but for the low numbers the success rate was pretty good. As we saw above, when
n
= 2, 3, 5 and 7 then 2
ⁿ
– 1 is prime.

The mathematician most fixated on using 2
ⁿ
– 1 to generate primes was the French friar Marin Mersenne. In 1644 he made the sweeping claim that he knew all the values of
n
up to 257 such that
²ⁿ
– 1 is prime. He claimed they were:

Mersenne was an able mathematician, but his list was largely based on guesswork. The number 2
²⁵⁷
– 1 is 78 digits long, far too big for the human mind to check whether it is prime or not. Mersenne realized that his numbers were stabs in the dark. He said of the list: ‘all time would not suffice to determine whether they are prime’.

Time did suffice, though, as it often does in the case of maths. In 1876, two and a half centuries after Mersenne wrote his list, the French number theorist Edouard Lucas devised a method that was able to check whether numbers written 2
ⁿ
– 1 are prime, and he found that Mersenne was wrong about 67 and that he had left out 61, 89 and 107.

Amazingly, however, Mersenne had been right about 127. Lucas used his method to prove that 2
¹²⁷
– 1, or 170,141,183,460,469,231, 731,687,303,715,884,105,727, was prime. This was the highest-known prime number until the computer age. Lucas, however, was unable to determine if 2
²⁵⁷
– 1 was prime or not; the number was simply too large to work on with pencil and paper.

Despite its patches of error, Mersenne’s list immortalized him; and now a prime that can be written in the form 2
ⁿ
– 1 is known as a
Mersenne prime
.

The proof of whether 2
²⁵⁷
– 1 is prime would take until 1952 to be proven, using the Lucas method, but with a big assist. A team of scientists gathered one day that year at the Institute for Numerical Analysis in Los Angeles to watch a 24ft scroll of tape be inserted into an early digital computer called the SWAC. Simply putting in the tape took several minutes. The operator then input the number to be tested: 257. In a fraction of a second came the result. Computer said no: 2
²⁵⁷
– 1 is not prime.

On the same evening in 1952 on which it was discovered that 2257 – 1 is not prime, new potential Mersenne numbers were inserted into the machine. The SWAC rejected the first 42 as not prime. Then, at 10 p.m., came a result. Computer said yes! It announced that 2
⁵²¹
– 1 is prime. The number was the highest Mersenne prime identified in 75 years, making the corresponding perfect number, 2520 (2
⁵²¹
– 1), only the thirteenth discovered in almost twice as many centuries. But the number 2
⁵²¹
– 1 had only two hours to enjoy its status as top of the pile. Shortly before midnight the SWAC confirmed that 2
⁶⁰⁷
– 1 was also prime. Over the next few months, SWAC worked to the limit of its capacities, finding three more primes. Between 1957 and 1996 another 17 Mersenne primes were discovered.

Since 1952, the largest-known prime number has always been a Mersenne prime (apart from a three-year interlude between 1989 and 1992 when the largest prime was (391581×2
^{216193p>) – 1, which is a related type of prime). Among all the primes that exist, and we know there is an infinite number of them, Mersenne primes dominate the table of highest discovered primes because they give prime-hunters a target to aim for. The best technique for finding high primes is to look for Mersenne primes, in other words, to put the number 2
n
– 1 into a computer for higher and higher values of
n
and use the Lucas-Lehmer test, an improved version of Edouard Lucas’s method mentioned earlier, to see if it is prime.}

Mersenne primes also have an aesthetic loveliness. For example, in binary notation any number 2
ⁿ
is written as 1 followed by
n
zeros. For example, 2
²
= 4, which in binary notation is written 100, and 2
⁵
= 32, which is written 100000. Since all Mersenne primes are 1 less than 2
ⁿ
, all binary expansions of Mersenne primes are strings of digits that contain only 1s.

The most influential prime-hunter of modern times was inspired in his mission by the markings on an envelope. When George Woltman was a boy, in the 1960s, his father showed him a postmark with the expression 2
¹¹²¹³
– 1, then the most recently calculated prime number. ‘I was amazed that a number so large could be proven prime,’ he remembered.

Woltman was later responsible for writing some software that has made an enormous contribution to the quest for primes. All projects that involved massive number-crunching used to be carried out on ‘supercomputers’, access to which was limited. Since the 1990s, however, many big tasks have been salami-sliced by dividing up the work among thousands of smaller machines connected to each other by the internet. In 1996 Woltman wrote a piece of software that users can download for free and that, once installed, allocates a small part of the uninvestigated number line where your machine can look for primes. The software uses the processor only when your computer is otherwise idle. While you are fast asleep, your machine is busy churning through numbers on the frontier of science. The Great Internet Mersenne Prime Search, or GIMPS, currently links about 75,000 computers. Some of these are in academic institutions, some are in businesses and some are personal laptops. GIMPS was one of the first ‘distributed computing’ projects and has been one of the most successful. (The largest similar project, Seti@home, is deciphering cosmic noise for signs of extraterrestrial life. It claims three million users but, so far, has discovered nothing.) Only a few months after GIMPS went online a 29-year-old French programmer netted the 35th Mersenne prime: 2
^1398269
– 1. Since then, GIMPS has revealed another 11 Mersenne primes, which is an average of about one a year. We are living in a golden age of high prime numbers.

The current record for largest prime is held by the 45th Mersenne prime: 2
^43112609
– 1, which is a number almost 13 million digits long, found in 2008 by a computer connected to GIMPS at the University of California, Los Angeles. The 46th and 47th Mersennes found were actually
smaller
than the 45th. This happened because computers are working at different speeds on different sections of the number line at the same time, so it is possible that primes in higher sections will be discovered before primes in lower ones.

GIMPS’s message of mass voluntary cooperation for scientific advancement has made it an icon of the liberal web. Woltman has unintentionally turned the search for primes into a quasi-political pursuit. As a mark of the symbolic importance of the project, the Electronic Frontier Foundation, a digital-rights campaign group, has since 1999 offered money for each prime whose digits reach the next order of magnitude. The 45th Mersenne prime was the first to hit ten million digits and the prize money won was $100,000. The EFF is offering $150,000 for the first prime with 100 million digits, and $250,000 for the first prime with a billion digits. If you plot the largest-known primes discovered since 1952 on a graph with a logarithmic scale against the time of discovery, they fall on what is almost a straight line. As well as showing how the growth of processing power has advanced remarkably consistently over time, the line also allows us to estimate when the first billion-digit prime will be discovered. I’d put money on it being found by 2025. Writing out this number in type where each digit is a millimetre would stretch further than from Paris to Los Angeles.

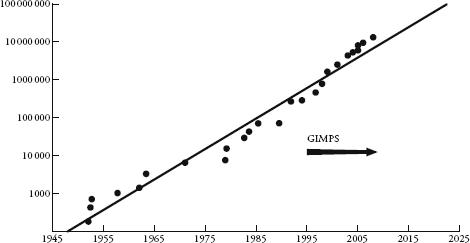
Digits in highest-known prime by year of discovery.

With an infinite number of primes (whether there is an infinite number of Mersenne primes, however, is not yet known), the search for higher and higher primes is a never-ending task. Whatever prime number we reach, no matter how large, there will always be a prime number even larger taunting us for our lack of ambition.

Endlessness is probably the most profound and challenging idea of basic maths. The mind finds it difficult to cope with the idea of something going on for ever. What, for example, would happen if we start counting 1, 2, 3, 4, 5…and never stop? I remember asking this seemingly simple question as a child, and receiving no straightforward answer. The default response from parents and schoolteachers was that we get to ‘infinity’ but this answer essentially just restates the question. Infinity is simply defined as being the number that we get to when we start counting and never stop.

Nevertheless, we are told from a relatively early age to treat infinity like a number, a weird number, but a number all the same. We are shown the symbol for infinity, the endless loop 8 (called a ‘lemniscate’), and taught its peculiar arithmetic. Add any finite number to infinity and we get infinity. Subtract any finite number from infinity and we get infinity. Multiply or divide infinity by a finite number, as long as it isn’t zero, and the result is also infinity. The ease with which we are told that infinity is a number disguises more than 2000 years of struggling to come to terms with its mysteries.

The first person to showcase the trouble with infinity was the Greek philosopher Zeno of Elea, who lived in the fifth century bc. In one of his famous paradoxes, he described a theoretical race between Achilles and a tortoise. Achilles is faster than the tortoise, so the tortoise is given a head start. The famous warrior starts at a point A and his reptile challenger is ahead of him at a point B. Once the race starts, Achilles zooms forward and soon reaches point B, but by the time he gets there, the tortoise has already advanced to point C. Achilles then ploughs on to point C. But once again, when he reaches this point, the tortoise has shuffled forward to point D. Achilles must reach D, of course, but when he does, the tortoise is already at E. Zeno argued that the game of catch-up must carry on for ever and, therefore, that swift Achilles is never able to overtake his slower four-footed rival. The athlete is much faster than the tortoise, but he cannot beat him in a race.