Alex’s Adventures in Numberland (66 page)

If the characteristics of a population are normally distributed, in other words are clustered around an average in the shape of a bell curve, and if the bell curve is produced through random error, then, Quételet argued, the variation in human characteristics can be seen as errors from a paradigm. He called this paradigm
l’homme moyen
, or ‘the average man’. Populations, he said, were made up of deviations from this prototype. In Quételet’s mind, being average was something to aspire to since it was a way of keeping society in check – deviations from the average, he wrote, led to ‘ugliness in body as well as vice in morals’. Even though the concept of
l’homme moyen
never gained acceptance in science, its use filtered down to society at large. We often talk about morality or taste in terms of what an average representative of a population might think or feel about it: such as what is seen as acceptable ‘in the eyes of the average man’.

Whereas Quételet extolled averageness, Galton looked down on it. Galton, as I mentioned before, saw that exam results were normally distributed. Most people scobout average, while a few got very high marks and a few very low.

Galton, incidentally, was himself from a very above-average family. His first cousin was Charles Darwin, and the two men corresponded regularly about their scientific ideas. About a decade after Darwin published
On the Origin of Species
, which set out the theory of natural selection, Galton started to theorize on how human evolution itself could be guided. He was interested in the heritability of cleverness and wondered how it might be possible to improve the overall intelligence of a population. He wanted to shift the bell curve to the right. To this end Galton suggested a new field of study about the ‘cultivation of race’, or improving the intellectual stock of a population through breeding. He had thought to call his new science
viticulture
, from the Latin
vita
, ‘life’, but eventually settled on
eugenics
, from the Greek
eu
, good, and
genos
, birth. (The usual meaning of ‘viticulture’, grape cultivation, comes from
vitis
, Latin for ‘vine’, and dates from around the same time.) Even though many liberal intellectuals of the late nineteenth and early twentieth centuries supported eugenics as a way to improve society, the desire to ‘breed’ cleverer humans was an idea that was soon distorted and discredited. In the 1930s eugenics became synonymous with murderous Nazi policies to create a superior Aryan race.

In retrospect, it is easy to see how ranking traits – such as intelligence or racial purity – can lead to discrimination and bigotry. Since the bell curve appears when human features are measured, the curve has become synonymous with attempts to classify some humans as intrinsically better than others. The highest-profile example of this was the publication in 1994 of
The Bell Curve
by Richard J. Herrnstein and Charles Murray, one of the most fiercely debated books of recent years. The book, which owes its name to the distribution of IQ scores, argues that IQ differences between racial groups are evidence of biological differences. Galton wrote that the bell curve reigned with ‘serenity and in complete self-effacement’. Its legacy, though, has been anything but.

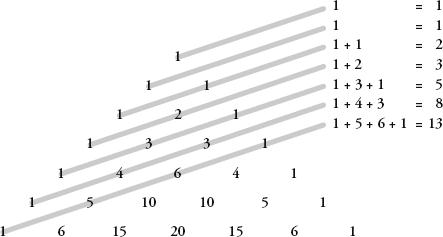
Another way to appreciate the lines of numbers produced by the quincunx is to lay them out like a pyramid. In this form, the results are better known as Pascal’s triangle.

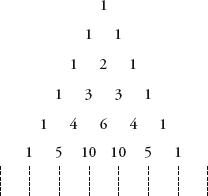
Pascal’s can be constructed much more simply than by working out the distributions of randomly falling balls through a Victorian bean machine. Start with a 1 in the first row, and under it place two 1s so as to make a triangle shape. Continue with subsequent rows, always placing a 1 at the beginning and end of the rows. The value of every other position is the
sum
of the two numbers above it.

Pascal’s triangle with only squares divisible by 2 in white.

The triangle is named after Blaise Pascal, even though he was a latecomer to its charms. Indian, Chinese and Persian mathematicians were all aware of the pattern centuries before he was. Unlike its prior fans, though, Pascal wrote a book about what he called
le triangle arithmétique
. He was fascinated by the mathematical richneshe patterns he discovered. ‘It is a strange thing how fertile it is in properties,’ he wrote, adding that in his book he had to leave out more than he could put in.

My favourite feature of Pascal’s triangle is the following. Let each number have its own square, and colour all the odd number squares black. Keep all the even-number squares white. The result is the wonderful mosaic above.

Hang on minute, I hear you say. This pattern looks familiar. Correct. It is reminiscent of the Sierpinski carpet, the piece of mathematical upholstery from p. 105 in which a square is divided into nine subsquares and the central one removed, with the same process being repeated to each of the subsquares ad infinitum. The triangular version of the Sierpinski carpet is the Sierpinski triangle, in which an equilateral triangle is divided into four identical equilateral triangles, of which the middle one is removed. The three remaining triangles are then subject to the same operation – divide into four and remove the middle one. Here are the first three iterations:

If we extend the method of colouring Pascal’s triangle to more and more lines, the pattern looks more and more like the Sierpinski triangle. In fact, as the limit approaches infinity, Pascal’s triangle
becomes
the Sierpinski triangle.

Sierpinski is not the only old friend we find in these black-and-white tiles. Consider the size of the white triangles down the centre of Pascal’s triangle. The first is made up of 1 square, the second is made up of 6 squares, the third is made of 28, and the next ones have 120 and 496 squares. Do these numbers ring any bells? Three of them – 6, 28 and 496 – are perfect numbers, from p. 265. The occurrence is a remarkable visual expression of a seemingly unrelated abstract idea.

Let’s continue painting Pascal’s triangle by numbers. First keep all numbers divisible by 3 as white, and make the rest black. Then repeat the process with the numbers that are divisible by 4. Repeat again with numbers divisible by 5. The results, shown opposite, are all symmetrical patterns of triangles pointing in the opposite direction to the whole.

In the nineteenth century, another familiar face was discovered in Pascal’s triangle: the Fibonacci sequence. Perhaps this was inevitable, as the method of constructing of the triangle was recursive – we repeatedly performed the same rule, which was the adding of two numbers on one line to produce a number on the next line. The recursive summing of two numbers is exactly what we do to produce the Fibonacci sequence. The sum of two consecutive Fibonacci numbers is equal to the next number in the sequence.

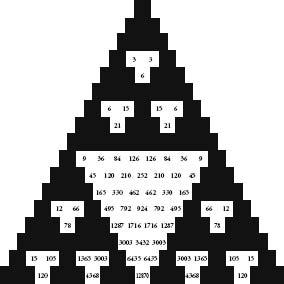
Pascal’s triangle with only squares divisible by 3 in white.

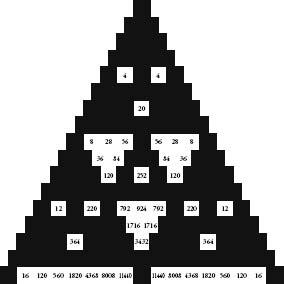
Pascal’s triangle with only squares divisible by 4 in white.

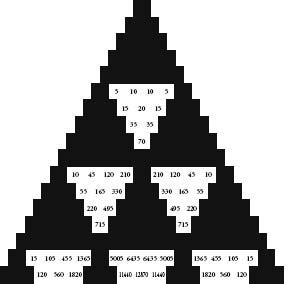
Pascal’s triangle with only squares divisible by 5 in white.