Alex’s Adventures in Numberland (61 page)

The first-ever random walk appeared in the third edition of John Venn’s
Logic of Chance
(1888). The rules for the direction of the walk (my addition) follow the digits 0–7 that appear in pi after the decimal point.

In Luke Rhinehart’s bestselling novel
The Dice Man
, the eponymous hero makes life decisions based on the throwing of dice. Consider Coin Man, who makes decisions based on the flip of a coin. Let’s say that if he flips heads, he moves one step up the page, and if he flips tails, he moves a step down the page. Coin Man’s path is a drunkard’s walk in one dimension – he can move only up and down the same line. Plotting the walk described by the second list of 30 coin flips chapter 9, you get the following graph.

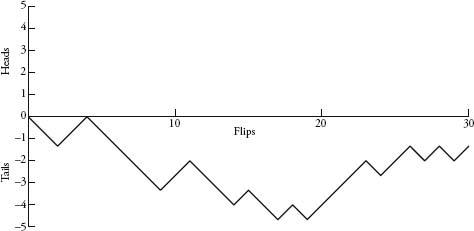
The walk is a jagged line of peaks and valleys. If you extended this for more and more flips, a trend emerges. The line swings up and down, with larger and larger swings. Coin Man roams further and further from his starting point in both directions. Below are the journeys of six coin men that I plotted from 100 flips each.

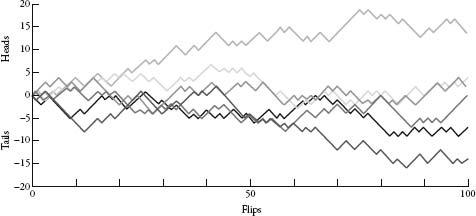
If we imagine that at a certain distance from the starting point in one direction there is a barrier, there is a 100 percent probability that eventually Coin Man will hit the barrier. The inevitability of this collision is very instructive when we analyse gambling patterns.

Instead of letting Coin Man’s random walk describe a physical journey, let it represent the value of his bank account. And let the coin flip be a gamble. Heads he wins £100, tails he loses £100. The value in his bank account will swing up and down in increasingly large waves. Let us say that the only barrier that will stop Coin Man playing is when the value of his account is £0. We know it is guaranteed he will get there. In other words, he will always go bankrupt. This phenomenon – that eventual impoverishment is a certainty – is known evocatively as
gambler’s ruin
.

Of course, no casino bets are as generous as the flipping of a coin (which has a payback percentage of 100). If the chances of losing are greater than the chances of winning, the map of the random walk drifts downward, rather than tracking the horizontal axis. In other words, bankruptcy looms quicker.

Random walks explain why gambling favours the very rich. Not only will it take much longer to go bankrupt, but there is also more chance that your random walk will occasionally meander upward. The secret of winning, for the rich or the poor, however, is knowing when to stop.

Inevitably, the mathematics of random walks contains some head-popping paradoxes. In the graphs chapter 9 where Coin Man moves up or down depending on the results of a coin toss, one would expect the graph of his random walk to regularly cross the horizontal axis. The coin gives a 50:50 chance of heads or tails, so perhaps we would expect him to spend an equal amount of time either side of his starting point. In fact, though, the opposite is true. If the coin is tossed infinitely many times, the most likely number of times he will swap sides is zero. The next most likely number is one, then two, three and so on.

For finite numbers of tosses there are still some pretty odd results. William Feller calculated that if a coin is tossed every second for a year, there is a 1-in-20 chance that Coin Man will be on one side of the graph for more than 364 days and 10 hours. ‘Few people believe that a perfect coin will produce preposterous sequences in which no change of [side] occurs for millions of trials in succession, and yet this is what a good coin will do rather regularly,’ he wrote in
An Introduction to Probability Theory and Its Applications
. ‘If a modern educator or psychologist were to describe the long-run case histories of individual coin-tossing games, he would classify the majority of coins as maladjusted.’

While the wonderful counter-intuitions of randomness are exhilarating to pure mathematicians, they are also alluring to the dishonourable. Lack of a grasp of basic probability means that you can easily be conned. If you are ever tempted, for example, by a company that claims it can predict the sex of your baby, you are about to fall victim to one of the oldest scams in the book. Imagine I set up a company, which I’ll call BabyPredictor, that announces a scientific formula for predicting whether a baby will be a boy or a girl. BabyPredictor charges mothers a set fee for the prediction. Because of a formidable confidence in its formula, and the philanthropic generosity of its CEO, me, the company also offers a total refund if the prediction turns out to be wrong. Buying the prediction sounds like a good deal – since either BabyPredictor is correct, or it is wrong and you can get your money back. Unfortunately, however, BabyPredictor’s secret formula is actually the tossing of a coin. Heads I say the child will be a boy, tails it will be a girl. Probability tells me that I will be correct about half the time, since the ratio of boys to girls is about 50:50. Of course, half the time I will give the money back, but so what – since the other half of the time I get to keep it.

The scam works because the mother is unaware of the big picture. She sees herself as a sample group of one, rather than as part of a larger whole. Still, baby-predicting companies are alive and well. Babies are born every minute, and so are mugs.

In a more elaborate version, this time targeting greedy men rather than pregnant women, a company we’ll call StockPredictor puts up a fancy website. It sends out 32,000 emails to an investors’ mailing list, announcing a new service, which, using a very sophisticated computer model, can predict whether a certain stock index will rise or fall. In half of the emails it predicts a rise the following week; and in the other half, a fall. Whatever happens to the index, 16,000 investors will have received an email with the correct prediction. So, StockPredictor then sends these 16,000 addresses another email with the following week’s prediction. Again, the prediction will be correct for 8000 of them. If StockPredictor continues like this for another four weeks, eventually there will be 1000 email recipients whose six consecutive predictions have all turned out to be true. StockPredictor then informs them that in order to receive any further predictions they must pay a fee – and why wouldn’t they, since the predictions have thus far been pretty good?

The stock-predicting scam can be adapted to predicting horse-races, football matches, and even the weather. If all outcomes are covered, there will be at least one person receiving a correct prediction of all matches, races or sunny days. That person might think, ‘Wow, there is only a one-in-a-million chance of such a combination being true,’ but if a million emails are sent out covering all possibilities, then someone, somewhere has to receive the correct one.

Scamming people is immoral and often illegal. However, trying to get one over on a casino is often seen as a just cause. For mathematicians, the challenge of beating the odds is like showing a red rag to a bull – and there is an honourable tradition of those who have succeeded.

The first method of attack is to realize that the world is not perfect. Joseph Jagger was a cotton-factory mechanic from Lancashire who knew enough about Victorian engineering to realize that roulette wheels might not spin perfectly true. His hunch was that if the wheel was not perfectly aligned, it might favour some numbers over others. In 1873, aged 43, he visited Monte Carlo to test his theory. Jagger hired six assistants, assigned each of them to one of the six tables in a casino, and instructed them to write down every number that came up over a week. Upon analysing the figures, he saw that one wheel was indeed biased – nine numbers came up more than others. The greater prevalence of these numbers was so slight that their advantage was only noticeable when considering hundreds of plays.

Jagger started betting and in one day won the equivalent of $70,000. Casino bosses, however, noticed that he gambled at only one table. To counter Jagger’s onslaught, they switched the wheels around. Jagger started to lose, until he realized what the management had done. He relocated to the biased table, which he recognized because it had a distinctive scratch. He started winning again and only gave up when the casino reacted a second time by sliding the frets around the wheel after each daily session, so that new numbers would be favoured. By that time Jagger had already amassed $325,000 – making him, in today’s terms, a multimillionaire. He returned home, left his factory job and invested in real estate. In Nevada, from 1949 to 1950, Jagger’s method was repeated by two science grads named Al Hibbs and Roy Walford. They started off with a borrowed $200 and turned it into $42,000, allowing them to buy a 40ft yacht and sail the Caribbean for 18 months before returning to their studies. Casinos now change wheels around much more regularly than they used to.

The second way to manipulate the odds in your favour is to question what randomness is anyway. Events that are random under one set of information might well become non-random under a greater set of information. This is turning a maths problem into a physics one. A coin flip is random because we don’t know how it will land, but flipped coins obey Newtonian laws of motion. If we knew exactly the speed and angle of the flip, the density of the air and any other relevant physical data, we would be able to calculate exactly the face on which it would land. In the mid 1950s a young mathematician named Ed Thorp began to ponder what set of information would be required to predict where a ball would land in roulette.

Thorp was helped in his endeavour by Claude Shannon, his colleague at the Massachusetts Institute of Technology. He couldn’t have wished for a better co-conspirator. Shannon was a prolific inventor with a garage full of electronic and mechanical gadgets. He was also one of the most important mathematicians in the world, as the father of information theory, a crucial academic breakthrough that led to the development of the computer. The men bought a roulette wheel and conducted experiments in Shannon’s basement. They discovered that if they knew the speed of the ball as it went around the stationary outer rim, and the speed of the inner wheel (which is spun in the opposite direction of the ball), they could make pretty good estimates regarding which segment of the wheel the ball would fall in. Since casinos allow players to place a bet after the ball has been dropped, all Thorp hannon needed to do was figure out how to measure the speeds and process them in the few seconds before the croupier closed the betting.

Once again, gambling pushed forward scientific advancement. In order to predict roulette plays accurately, the mathematicians built the world’s first wearable computer. The machine, which could fit in a pocket, had a wire going down to the shoe, where there was a switch, and another wire going up to a pea-sized headphone. The wearer was required to touch the switch at four moments – when a point on the wheel passed a reference point, when it had made one full revolution, when the ball passed the same point, and when the ball had again made a full revolution. This was enough information for estimating the speeds of the wheel and the ball.

Thorp and Shannon divided the wheel into eight segments of five numbers each (some overlapped, though, as there are 38 pockets). The pocket-sized computer played a scale of eight notes – an octave – through the headphones and the note it stopped on determined the segment where it predicted the ball would fall. The computer could not say with total certainty which segment the ball would land in, but it didn’t need to. All Thorp and Shannon desired was that the prediction would be better than the randomness of guessing. On hearing the notes, the computer-wearer would then place chips on all five numbers of the segment (which, although next to each other on the wheel, were not adjacent on the baize). The method was surprisingly accurate – for the single-number bets they estimated that they could expect to win $4.40 for every $10 wager.

When Thorp and Shannon went to Las Vegas for a test drive, the computer worked, if precariously so. The men needed to look inconspicuous, but the earpiece was prone to popping out and the wires were so fragile that they kept breaking. Still, the system worked, and they were able to convert a small pile of dimes into a few piles of dimes. Thorp was content to have beaten roulette in theory, if not in practice, because his assault on another gambling game was having much more striking success.