Alex’s Adventures in Numberland (73 page)
Read Alex’s Adventures in Numberland Online
Authors: Alex Bellos

On the third day, even more buses arrive at the Hilbert Hotel. In fact, an infinite number of buses arrives. The buses are lined up outside, with Bus 1 next to Bus 2, which is next to Bus 3, and so on. Each bus has an infinite number of passengers, like the bus that arrived the day before. And, of course, every passenger needs a room. Is there a way to find every passenger in every bus a room in the (already full) Hilbert Hotel?
No problem, says the receptionist. First, he needs to clear an infinite number of rooms. He does this by the trick he used the day before – move everyone to a room with twice the room number. This leaves all the odd-numbered rooms free. In order to fit in the infinite coach parties, all he needs to do is find a way of counting all the passengers, since once he has found a method, he can assign the first passenger to Room 1, the second to Room 3, the third to Room 5, and so on.
He does it like this: for each bus, list the passengers by seat, as in the table below. Each passenger is therefore represented by the form
m
/
n
where
m
is the number of the bus they are on and
n
is their seat number. If we start at the passenger in the first seat in the first bus (person 1/1), and then form the zigzag pattern below, by letting the second person be the passenger who is in the second seat of the first bus (1/2), and the third be the first passenger on the second (2/1), we will eventually count every single passenger.
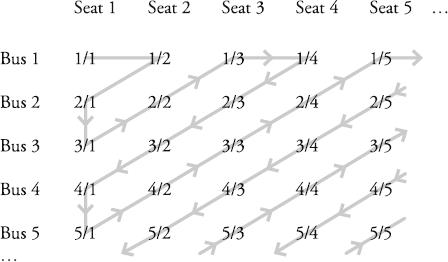
Now let’s translate what we have learned with the Hilbert Hotel into some symbolic mathematics:
When one person was found a room, this was the equivalent of showing that 1 +
=
When a countably infinite number of people could be found a room, we saw that
×
=
When a countably infinite number of buses, each containing a countably infinite number of passengers could be found a room, this revealed that
×
=
These rules are what we expect from infinity: add infinity to infinity and we get infinity, multiply infinity by infinity and we get infinity.
Let’s stop here a second. We have already reached an amazing result. Look again at the table of seats and buses. Consider each thenn denoted
m/n
as the fraction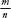 . The table, when extended infinitely, will cover every single positive fraction, since the positive fractions can also be defined as
. The table, when extended infinitely, will cover every single positive fraction, since the positive fractions can also be defined as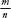 for all natural numbers
for all natural numbers
m
and
n
. For example, the fraction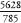 will be covered on the 5628th row and 785th column. The zigzag counting method that counted every passenger in every bus can, therefore, also be used to count every positive fraction. In other words, the set of all positive fractions and the set of natural numbers have the same cardinality, which is
will be covered on the 5628th row and 785th column. The zigzag counting method that counted every passenger in every bus can, therefore, also be used to count every positive fraction. In other words, the set of all positive fractions and the set of natural numbers have the same cardinality, which is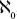 . It seems intuitive that there should be more fractions than there are natural numbers, since between any two natural numbers there is an infinite number of fractions, yet Cantor showed that our intuition is wrong. There are as many positive fractions as there are natural numbers. (In fact, there are as many positive and negative fractions as there are natural numbers, since there are
. It seems intuitive that there should be more fractions than there are natural numbers, since between any two natural numbers there is an infinite number of fractions, yet Cantor showed that our intuition is wrong. There are as many positive fractions as there are natural numbers. (In fact, there are as many positive and negative fractions as there are natural numbers, since there are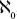 positive fractions and
positive fractions and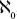 negative fractions and, as seen above,
negative fractions and, as seen above,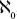 ×
×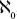 =
=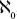 .)
.)