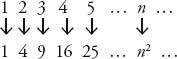Alex’s Adventures in Numberland (72 page)
Read Alex’s Adventures in Numberland Online
Authors: Alex Bellos
The reason why mathematicians pre-Cantor were nervous about treating infinity like any other number was that it contained many conundrums, the most famous of which Galileo wrote about in
Two New Sciences
, and is known as Galileo’s paradox:
1. Some numbers are squares, such as 1, 4, 9 and 16, and some are not squares, such as 2, 3, 5, 6, 7, etc.
2. The totality of all numbers must be greater than the total of squares, since the totality of all numbers includes squares and non-squares.
3. Yet for every number, we can draw a one-to-one correspondence between numbers and their squares, for example:
4. So, there are, in fact, as many squares as there are numbers. Which is a contradiction, since we have said, in point 2, that there are more numbers than squares.
Galileo’s conclusion was that, when it comes to infinityostmerical concepts ‘more than’, ‘equal to’ and ‘less than’ do not make sense. These terms may be understandable and coherent when discussing finite amounts, but not with infinite ones. It is meaningless to say there are more numbers than there are squares, or that there is an equal number of numbers and squares, since the totality of both numbers and squares is infinite.
Georg Cantor devised a new way to think about infinity that made Galileo’s paradox redundant. Rather than thinking about individual numbers, Cantor considered collections of numbers, which he called ‘sets’. The cardinality of any set is the number of members in the collection. So {1, 2, 3} is a set with a
cardinality
of three and {17, 29, 5, 14} is a set with cardinality four. Cantor’s ‘set theory’ gets the pulse racing when considering sets with an infinite number of members. He introduced a new symbol for infinity,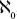
, (pronounced
aleph-null
), using the first letter of the Hebrew alphabet with the subscript 0, and said that this was the cardinality of the set of natural numbers, or {1, 2, 3, 4, 5…}. Every set whose members can be put in a one-to-one correspondence with the natural numbers also has cardinality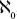. So, because there is a one-to-one correspondence between the natural numbers and their squares, the set of squares {1, 4, 9, 16, 25…} has cardinality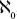. Likewise, the set of odd numbers {1, 3, 5, 7, 9…}, the set of prime numbers {2, 3, 5, 7, 11…} and the set of numbers with 666 in them {666, 1666, 2666, 3666…}, all have cardinality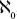. If you have a set with an infinite number of members, and it is possible to count its members one by one so that eventually every member will be reached, then the cardinality of the set is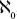. For this reason,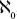is also known as a ‘countable infinity’. The reason this is exciting is because Cantor went on to show that we can go higher. Large though it may be,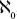is merely the baby in Cantor’s family of infinities.
I’ll introduce you to an infinity larger than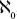with the help of a story David Hilbert is said to have used in his lectures that concerns a hotel with a countably infinite, or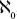, number of rooms. This well-known establishment, much loved by mathematicians, is sometimes called the Hilbert Hotel.
In the Hilbert Hotel there is an infinite number of rooms and they are numbered 1, 2, 3, 4…One day a traveller arrives at reception only to find that the hotel is full. He asks if there is any way a room can be found for him. The receptionist replies that of course there is! All the management needs to do is to reassign guests to different rooms in the following way: moving the guest in Room 1 to Room 2, moving the guest in Room 2 to Room 3, and so on, moving everyone in Room
n
to Room
n
+ 1. If this is done, then every guest still has a room, and Room 1 is freed up for the new arrival. Perfect!
The following day a more complicated situation presents itself. A bus arrives, with all the passengers needing rooms. This bus has an infinite number of seats, numbered 1, 2, 3 and so on, all of which are occupied. Is there any way that a room can be found for each and very one of the passengers? In other words, even though the hotel is full, can the receptionist reshuffle the guests into different rooms in a way that leaves an infinite number of free rooms for the bus passengers? Easy peasy, comes the reply. All the management needs to do this time is to move every guest to the room numbered double the room he or she is already in, which takes care of Rooms 2, 4, 6, 8…This leaves all the rooms with odd numbers empty, and the bus passengers can be given the keys for those. The passenger on the first seat gets Room 1, the first odd number, the passenger on the second seat gets Room 3, the second odd number, and so on.