Alex’s Adventures in Numberland (74 page)

We can appreciate how strange this result is by considering the number line, which is a way of understanding numbers by considering them as points on a line. Below is a number line starting at 0 and heading off towards infinity.

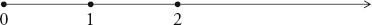
Every positive fraction can be considered as a point on this number line. From a previous chapter, we know that there is an infinite number of fractions between 0 and 1, as there is between 1 and 2, or between any two other numbers. Now imagine holding a microscope up to the line so that you can see between the points representing the fractions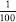
and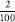
. As we also showed earlier, there is an infinite number of points representing fractions between these two points. In fact, wherever you place your microscope on the line, and however tiny the interval between two points that your microscope can see, there will always be infinitely many points representing fractions in this interval. Since there are infinite numbers of points representing fractions wherever you look, it comes as a bewildering surprise to realize that it is, in fact, possible to count them in an ordered list that will cover every single one without exception.

Now for the big event: proof that there is a cardinality larger than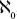
. Back we go to the Hilbert Hotel. On this occasion, the hotel is empty when an infinite number of people show up wanting rooms. But this time the travellers have not come in buses; they are in fact a rabble, with each wearing a T-shirt displaying a decimal expansion of a number between 0 and 1. No two people have the same decimal expansion on their chest and every single decimal expansion between 0 and 1 is covered. (Of course, the decimal expansions are infinitely long and so the T-shirts would need to be infinitely wide to display them, yet since we have suspended our disbelief in order to imagine a hotel with an infinite number of rooms, I figure it is not asking too much to envisage these T-shirts.)

A few of the arrivals charge into reception and ask if there is a way the hotel can accommodate them. For the receptionist to achieve this all he needs to do is find a way of listing every single decimal between 0 and 1, since once he has listed them, he can assign them rooms. This seems like a fair challenge, since, after all, he was able to find a way to list an infinite number of passengers from an infinite number of buses. This time, however, the task is impossible. There is no way to count every single decimal expansion between 0 and 1 in such a way that we can write them all down in an ordered list. To prove this I will show that for every infinite list of numbers between 0 and 1 there will always be a number between 0 and 1 that is not on the list.

This is how it’s done. Let’s imagine the first arrival has a T-shirt with the expansion 0.6429657…, the second has 0.0196012…, and the receptionist assigns them rooms 1 and 2. And say he carries on assigning rooms to the other arrivals, thus creating the infinite list that begins (remember, each of these expansions goes on for ever):

Our aim, stated earlier, is to find a decimal expansion between 0 and 1 that is not on this list. We do this using the following method. First, construct the number that has the first decimal place of the number in Room 1, the second decimal place of the number in Room 2, the third decimal place of the number in Room 3 and so on. In other words, we are selecting the diagonal digits that are underlined here:

This number is:

0.6182811…

We’re almost there. We now need to do one final thing to construct our number that is not on the receptionist’s list: we alter every digit in this number. Let’s do this by adding 1 to every digit, so the 6 becomes a 7, the 1 becomes a 2, the 8 becomes a 9, and so on, to get this number: 0.7293922…

And now we have it. This decimal expansion is the exception that we were looking for. It cannot be on the receptionist’s list because we have artificially constructed it so it cannot be. The number is not in Room 1, because its first digit is different from the first digit of the number in Room 1. The number is not in Room 2 because its second digit is different from the second digit of the number in Room 2, and we can continue this to see that the number cannot be in any Room
n
because its
n
th digit will always be different from the
n
th digit in the expansion of Room
n
. Our customized expansion 0.7293922…therefore cannot be equal to any expansion assigned to a room since it will always differ in at least one digit from the expansion assigned to that room. There may well be a number in the list whose first seven decimal places are 0.7293922, yet if this number is on the list then it will differ from our customized number by at least one digit further down the expansion. In other words, even if the receptionist carries on assigning rooms for ever and ever, he will be unable to find a room for the arrival with the T-shirt marked with the number we created beginning 0.7293922…

I chose a list starting with the arbitrary numbers 0.6429657…and 0.0196012…but equally I could have chosen a list starting with any numbers. For every list that it is possible to make, it will always be possible to create, using the ‘diagonal’ method opposite, a number that is not on the list. The Hilbert Hotel may have an infinite number of rooms, yet it
cannot
accommodate the infinite number of people defined by the decimals between 0 and 1. There will always be people left outside. The hotel is simply not big enough.

Cantor’s discovery that there is an infinity
bigger
than the infinity of natural numbers was one of the greatest mathematical breakthroughs of the nineteenth century. It is a mind-blowing result, and part of its power is that the result really was quite straightforward to explain: some infinities are countable, and they have size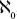
, and some infinities are not countable, and hence bigger. These uncountable infinities come in many different sizes.

The easiest uncountable infinity to understand is called
c
and is the number of people who arrived at the Hilbert Hotel with T-shirts containing all the decimal expansions between 0 and 1. Again, it is instructive to interpret
c
by looking at what it means on the number line. Every person with a decimal expansion between 0 and 1 on his T-shirt can also be understood as a point on the line between 0 and 1. The initial
c
is used since it stands for the ‘continuum’ of points on a number line.

And here217;s where we come to another strange result. We know that there are
c
points between 0 and 1, and yet we know that there are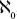
fractions on the totality of the number line. Since we have proved that
c
is bigger than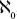
, it must be the case that there are more points on a line between 0 and 1 than there are points that represent fractions on the entire number line.