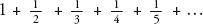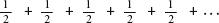Alex’s Adventures in Numberland (77 page)

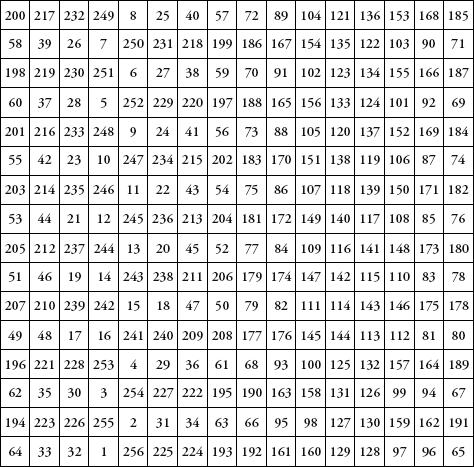
In Franklin’s 16 × 16 magic square all the lines and columns add up to 2056. It is not a true magic square since the diagonals do not add up to 2056, but it is so rich in prope
rties that Clifford A. Pickover writes that ‘it is no exaggeration to say that one could spend a lifetime contemplating its wonderful structure’. For example, every 2 × 2 subsquare (and there are 225 of those) adds up to 514, which means that every 4 × 4 subsquare adds up to 2056. Many other symmetries and patterns are also contained in the square.

The principle behind Gijswijt’s sequence is to look for repeating blocks of numbers in the previous terms of the sequence. The ‘block’ has to be at the end of the sequenc
e of previous terms, and the number of times it is repeated provides the next term.

Mathematically, the sequence is described as follows. Start with a 1, and then each subsequent term is the value
k
, when the previous terms are multiplied in order and written
xy
^k
for the largest possible value of
k
.

The sequence is 1, 1, 2, 1, 1, 2, 2, 2, 3, 1, 1, 2, 1, 1, 2, 2, 2, 3, 1, 1…

I think it is easiest to understand what is at work here by considering the first time a 3 appears, which is in position 9. The previous terms multiplied in order are 1 × 1 × 2 × 1 × 1 × 2 × 2 × 2. What Gijswijt requires us to do is to transform this sum into a term
xy
^k
for the largest value of
k
. In this case, we get (1 × 1 × 2 × 1 × 1) × 2
³
. So, the following term is a 3. We are looking for the largest repeating block of numbers at the end of the sequence of previous terms, although in this case the block is a single number, 2, repeated three times.

But often the block will have several digits. Consider position 16. The previous terms multiplied tther are 1 × 1 × 2 × 1 × 1 × 2 × 2 × 2 × 3 × 1 × 1 × 2 × 1 × 1 × 2. This can be written (1 × 1 × 2 × 1 × 1 × 2 × 2 × 3) × (1 × 1 × 2)
²
. So, the 16th term is a 2.

Going back to the beginning now, the second term is a 1 since the previous term 1 is not multiplied by anything. The third term is a 2 since the previous terms multiplied in order are 1 × 1 = 1
²
, and the fourth term is 1 since the previous terms result in (1 × 1 × 2) × 1, where the final 1 is not multiplied by itself.

We want to show that the harmonic series diverges, in other words that

will add up to infinity. This is done by showing that the harmonic series is larger than the following series, which does add up to infinity:

Let’s compare terms of the harmonic series in groups of two, four, eight and so on, starting from the third term. They are listed below. Because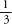
is bigger than
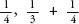must be bigger than
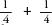which is
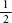. Likewise, since
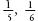and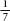
are all bigger than
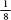, this means that
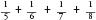is bigger than four eighths, which is also
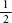. If we carry on, always considering double the number of terms, we can see that we will be able to add up these terms to make a value larger than
:

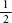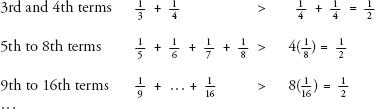
The harmonic series, therefore, is bigger than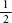
+
+
+
+
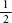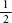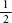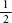+ …, which is infinity times a half, which is infinity. So the harmonic series is bigger than infinity; in other words, it is infinite.