Alex’s Adventures in Numberland (76 page)

In order to see how Annairizi’s tiled squares prove Pythagoras’s Theorem, look at the marked triangle chapter 2. All that we need to do is to rearrange the square of the hy
potenuse into precisely the squares of the other two sides. The square of the hypotenuse is made up of five sections; three are light grey and two are dark grey. We can see by considering how the pattern repeats that the light grey sections make up exactly the square of one of the sides of the triangle, and that the dark grey sections make up the square of the other side.

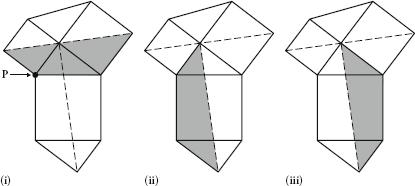
For Leonardo’s proof, first we need to show that the shaded sections in (i) and (ii) below are equal. We do this by rotating the section around point P. The two sections have >Iname side lengths and angles and therefore must be the same. Then we need to show that this section is equal to the section in (iii). This must be true since it is made up of identical parts.

With this information, we can complete the proof. The reflection of the first shaded section and its mirror image across the dotted line consists of two identical right-angled triangles and the squares on its two smaller sides. This area must be equal to the area covered by the sections shaded in (ii) and (iii) together, which consists of two identical right-angled triangles and the square of the hypotenuse. If we subtract the area of two triangles from both of these cases, the square of the hypotenuse must be equal to the square on the other two sides.

In a unit square, the diagonal has length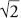
. To show that this is irrational I will use a
proof by contradiction
in which it is assumed that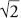
is rational, and then I will show how this leads to a contradiction. If it is contradictory to say that
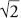is rational, it must be irrational.

If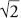
is rational, then there are natural numbers
a
and
b
, such that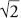
=
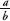. Let’s insist that this is the most reduced form of the fraction, so there is no way of rewriting
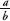as
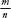when
m
and
n
are natural numbers less than
a
and
b
.

If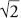
=
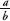, then by squaring both sides of the equation, 2 =
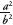which we can rewrite as
a
²
= 2
b
²
.

Whatever the value of
b
²
, 2
b
²
must be even since multiplying any natural number by two makes an even number. If 2
b
²
is even, then a2 is even. Now, since the square of an odd number is always an odd number, and the square of an even number is always even, this means that
a
must be even.

If
a
is even, then there is a number
c
less than
a
such that
a
= 2
c
, and therefore that
a
²
= (2
c
)
²
= 4
c
²
.

By replacing
a
²
with 4
c
²
in the equation above, we get 4
c
²
= 2
b
²
. Which reduces to
b
²
= 2
c
²
. By the same reasoning, this means that b2 is even, so
b
is even. If
b
is even, there is a number
d
less than
b
such that
b
= 2
d
p>

Therefore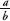
can be rewritten
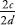, or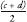
since the 2s cancel. We have our contradiction! From above we have stipulated that
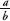is the most reduced form of the fraction, which means that there are no values for
c
and
d
less than
a
and
b
such that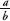
=
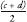. Since we have arrived at a contradiction by assuming that
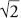can be written as
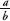it must be the case that
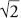cannot be written in such a way, so
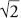is irrational.