Alex’s Adventures in Numberland (71 page)

Figure 2

Poincaré’s discworld is illuminating, but only up to a point. While it provides us with a conceptual model of hyperbolic space, distorted through a rather strange lens, it does not reveal what a hyperbolic surface looks like in our world. The search for more realistic hyperbolic models, which had looked promising in the last decades of the nineteenth century, was dealt a blow by the German mathematician David Hilbert in 1901, when he proved that it was impossible to describe a hyperbolic surface using a formula. Hilbert’s proof was accepted by the mathematical community with resignation, since they concluded that if there was no way of describing such a surface with a formula, then such a surface must not actually exist. Interest in coming up with models for hyperbolic surfaces waned.

Which brings us back to Daina Taimina, whom I met at the South Bank, a riverside promenade of theatres, art galleries and cinemas in London. She gave me a brief summary of the history of hyperbolic space, which is a subject she has taught in her position as adjunct associate professor at Cornell. A consequence of Hilbert’s proof that hyperbolic space cannot be generated by a formula, she said, is that computers are unable to create images of hyperbolic surfaces because computers can only create images based on formulas. In the 1970s, however, the geometer William Thurston found a low-tech approach to be much more fruitful. He had the idea that you didn’t need a formula to make a hyperbolic model – all you needed was paper and scissors. Thurston, who in 1981 was awarded the Fields Medal (the supreme prize in maths) and who is now a colleague of Daina’s at Cornell, came up with a model made from sticking together horseshoe-shaped slivers of paper.

Daina used a Thurston model with her students but it was so fragile that it always fell apart, and she had to make a new one each time. ‘I hate gluing paper. It drives me crazy,’ she said. Then she had a brainwave. What if it were possible to knit a model of the hyperbolic plane instead?

Her idea was simple: start with a line of stitches, and then for each subsequent line add a fixed amount relative to the number of stitches on the line before. For example, adding an extra stitch for every two stitches on the line before. In this case, if you started with a line of 20 stitches, the second line would have 30 stitches (adding 10), the third line 45 stitches (adding 15), and so on. (The fourth line should have an extra 22.5 stitches, but since you can’t do half stitches you have to round up or down.) This, she hoped, would create a piece of fabric that became wider and wider – as if expanding out from itself hyperbolically. However, the knitting was too fiddly, since after any mistake she needed to unravel the whole line. So she swapped the knitting needles for a crochet hook. With crochet, there is no chance of unravelling, as you progress one stitch at a time. She got the knack pretty quickly. It helped that Daina was a demon at craftwork, a consequence of a childhood in 1960s Soviet Latvia.

For her first crochet model she added an extra stitch for every two stitches on the previous line. The result, however, was a piece of material with many tight ruffles. ‘It was too curly,’ she said. ‘I couldn’t see what was going on.’ So for her next attempt, she changed the ratio, adding an extra stitch only for every five on the previous line. It worked better than she had expected. The material was now properly folding in on itself. She picked it up and followed straight lines in and out of the expanding flaps, and quickly realized that she could see parallel lines that diverged. ‘It was the picture I always wanted to see,’ she beamed. ‘That was my excitement. It was also a quick thrill to make something with my hands that cannot be made by computer.’

Daina showed the hyperbolic crochet model to her husband – and he was as excited as she was. David Henderson is professor of geometry at Cornell. His specialism is topology, which Daina claims to know nothing about. He explained to her that topologists have long known that when an octagon is drawn on the hyperbolic plane it can be folded together in such a way as to resemble a pair of pants. ‘We have to construct that octagon!’ he told her, which is just what they did. ‘No one had seen a hyperbolic pair of pants before!’ Daina exclaimed, and opened a sports bag she had with her, took out a crocheted hyperbolic octagon and folded it to show me the model. It looked liht liery cute pair of woollen toddler’s shorts:

Word spread around the Cornell maths faculty about Daina’s threaded creations. She told me she showed it to one colleague who is known for writing about hyperbolic planes. ‘He looked at the model and started playing with it. Then his face lit up. “This is what a
horocycle
looks like!” he said,’ having recognized a very complicated type of curve that he had never been able to picture before. ‘He had been writing about them all his career,’ added Daina, ‘but they were all in his imagination.’

It is no exaggeration to say that Daina’s hyperbolic models have given important new insight into a conceptually punishing area of maths. They give a visceral experience of the hyperbolic plane, allowing students to touch and feel a surface that was previously understood only in an abstract way. The models are not perfect, however. One problem is that the thickness of the stitches makes the crocheted models only a rough approximation of what in theory should be a smooth surface. Still, they are a great deal more versatile and accurate than a Pringle. If a piece of hyperbolic crochet had an infinite number of lines, it would theoretically be possible to live on that surface and walk for ever in one direction without ever coming to an edge.

One of the charms of Daina’s models is that they are unexpectedly organic-looking for something conceived so formally. When the relative line-by-line increase in stitches is small, the models look like leaves of kale. When the increase is greater the material naturally folds itself into pieces that look like coral. In fact, the reason Daina came to London was for the opening of the Hyperbolic Crochet Coral Reef, an exhibition inspired by her models to promote awareness of marine destruction. Thanks to her mathematical innovation, she has unwittingly spawned a global movement of crochet activism.

Over the last decade, Daina has crocheted more than a hundred hyperbolic models. She brought her largest to London. It is pink, uses 5.5km of yarn, weighs 4.5kg and took her six months. Finishing it was an ordeal. ‘As it got bigger it took a lot of energy to turn.’ A remarkable property of the model is that it has an incredibly large surface area – 3.2 square metres, which is twice as much surface area as Daina herself. Hyperbolic surfaces maximize area with minimal volume, which is why they are favoured by some plants and marine organisms. When an organism needs a large surface area – to absorb nutrition, as is the case with coral – it grows in a hyperbolic way.

It is unlikely that Daina would ever have thought up the idea of hyperbolic crochet had she been born a man, which makes her inventions a noteworthy artefact in the cultural history of mathematics, where women have long been under-represented. Crochet, in fact, is just one example of a traditionally female craft inspiring mathematicians in recent years to explore new techniques. Together with mathematical knitting, quilt-making, embroidery and weaving, the academic discipline is now known as Math and the Fiber Arts.

When hyperbolic space was first conceived it appeared to go against any sense of reality, yet it has become accepted as equally ‘real’ as flat or spherical surfaces. Every surface has its own geometry, and we need to choose the one that best applies, or, as Henri Poincaré once said: ‘One geomtry cannot be more true than another; it can only be more convenient.’ Euclidean geometry, for example, is the most appropriate for schoolchildren armed with rulers, compasses and flat pieces of paper, while spherical geometry is the most appropriate for airline pilots navigating flight paths.

Physicists are also interested in which geometry is most appropriate for their purposes. Riemann’s ideas about the curvature of surfaces provided Einstein with the equipment to make one of his greatest breakthroughs. Newtonian physics assumed that space was Euclidean, or flat. Einstein’s theory of general relativity, however, stated that the geometry of space-time (3-D space plus time considered as the fourth dimension) was not flat but curved. In 1919 a British scientific expedition in Sobral, a town in the northeast of Brazil, took images of the stars behind the sun during a solar eclipse and found that they had shifted slightly from their real positions. This was explained by Einstein’s theory that the light from the stars was curving a round the sun before it reached Earth. While the light appeared to bend around the sun when seen in three-dimensional space, which is the only way we can see things, it was actually following a straight line according to the curved geometry of space-time. The fact that Einstein’s theory correctly predicted the position of the stars vindicated his general theory of relativity and it is what made him a global celebrity. The London
Times
headline blazoned: ‘Revolution in Science, New Theory of the Universe, Newtonian Ideas Overthrown’.

Einstein was concerned with space-time, which he showed to be curved. What about the curvature of our universe without considering time as a dimension? In order to see which geometry best fits the behaviour of our three spatial dimensions on a large scale, we need to see how lines and shapes behave over extremely large distances. Scientists are hoping to discover this from the data that is being gathered by the Planck satellite, launched in May 2009, which is measuring cosmic background radiation – the so-called ‘afterglow’ of the Big Bang – to a higher resolution and sensitivity than ever before. Considered opinion is that the universe is either flat or spherical, although it is still possible that the universe might be hyperbolic. It is wonderfully ironic to think that a geometry originally thought to be nonsensical might actually reflect the way things really are.

At around the same time that mathematicians were exploring the counter-intuitive realm of non-Euclidean space, one man was turning upside-down our understanding of another mathematical notion: infinity. Georg Cantor was a lecturer at Halle University in Germany, where he developed a trail-blazing theory of numbers in which infinity could have more than one size. Cantor’s ideas were so unorthodox that they initially provoked ridicule from many of his peers. Henri Poincaré, for example, described his work as ‘a malady, a perverse illness from which some day mathematics would be cured’, while Leopold Kronecker, Cantor’s former teacher and professor of maths at Berlin University, dismissed him as a ‘charlatan’ and a ‘corruptor of youth’.

This war of words probably contributed to Cantor’s nervous breakdown in 1884, aged 39, the first of many mental-health episodes and hospitalizations. In his book on Cantor,
Everything and More
, David Foster Wallace writes: ‘The Mentally Ill Mathematician seems now in some ways to be what the Knight Errant, Mortified Saint, Tortured Artist, and Mad Stist have been for other eras: sort of our Prometheus, the one who goes to forbidden places and returns with gifts we can all use but he alone pays for.’ Literature and film are guilty of romanticizing a link between maths and insanity. It’s a cliché that suits the narrative requirements of a Hollywood script (exhibit A:
A Beautiful Mind
) but is, of course, an unfair generalization. The great mathematician, however, for whom the archetype could have been invented is Cantor. The stereotype fits him especially well since he was grappling with infinity, a concept that links mathematics, philosophy and religion. Not only was he challenging mathematical doctrine, but he was also setting out a brand-new theory of knowledge and, in his mind, of human understanding of God. No wonder he upset a few people along the way.

Infinity is one of the most brain-mangling concepts in maths. We saw earlier, in our discussion of Zeno’s paradoxes, that envisaging an infinite number of ever-decreasing distances is full of mathematical and philosophical pitfalls. The Greeks tried to avoid infinity as much as they could. Euclid expressed ideas of infinity by making negative assertions. His proof that there is an infinite number of prime numbers, for instance, is actually a proof that there is no highest prime number. The ancients shied away from treating infinity as a self-contained concept, which is why the infinite series inherent in Zeno’s paradoxes were so problematic for them.

By the seventeenth century, mathematicians were willing to accept operations involving an infinite number of steps. The work of John Wallis, who in 1655 introduced the symbol 8 for infinity for the purpose of his work on infinitesimals (things that become infinitely small), paved the way for Isaac Newton’s calculus. The discovery of useful equations that involved an infinite number of terms, such as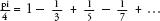
…showed that infinity was not an enemy, yet even so, it was still to be treated with care and suspicion. In 1831 Gauss stated the received wisdom when he said that infinity was ‘merely a way of speaking’ about a limit that one never reached, an idea that simply expressed the potential to carry on and on for ever. Cantor’s heresy was to treat infinity as an entity in itself.