Alex’s Adventures in Numberland (35 page)
Read Alex’s Adventures in Numberland Online
Authors: Alex Bellos

Significantly, the only piece of calculation we have done to work out this multiplication was a fairly simple addition.
Logarithms, wrote Napier, were able to free mathematicians from the ‘tedious expense of time’ and the ‘slippery errors’ involved in the ‘multiplications, divisions, square and cubical extractions of great numbers’. Using Napier’s invention, not only could multiplication be made into the addition of logs, but division was made into the subtraction of logs; calculating of square roots was made into the division of logs by two; and calculating cube roots, into the division of logs by three.
The convenience that logarithms brought made them the most significant mathematical invention of Napier’s time. Science, commerce and industry benefited massively. The German astronomer Johannes Kepler, for example, used logs almost immediately to calculate the orbit of Mars. It has recently been suggested that he might not have discovered his three laws of celestial mechanics without the ease of calculation offered by Napier’s new numbers.
In his 1614 book
A Description of the Admirable Table of Logarithmes
, Napier used a slightly different version of logarithms than those used in modern mathematics. Logarithms can be expressed as a power of any number, which is called the base. Napier’s system used an unnecessarily complicated base of 1 – 10
–7
(which he then multiplied by 10
7
). Henry Briggs, England’s top mathematician in Napier’s day, visited Edinburgh to congratulate the Scot on his discoveries. Briggs went on to simplify the system by introducing base-ten logarithms – which are also known as Briggsian logarithms, or common logarithms, because ten has been the most popular base ever since. In 1617 Briggs published a table of the logs of all numbers from 1 to 1000 to eight decimal places. By 1628 Briggs and the Dutch mathematician Adriaan Vlacq had extended the log table to 100,000, to ten decimal places. Their calculations involved laborious number-crunching – although, once the sums were done correctly, they never needed to be done again.
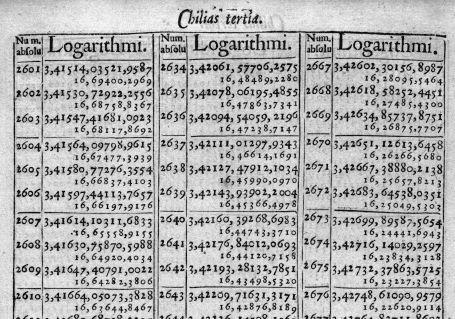
Page of Briggs’s log tables from 1624.
That is, until 1792, when the young French republic decided to commission ambitious new tables – the log of every number to 100,000 to 19 decimal places,nd rom 100,000 to 200,000 to 24 decimal places. Gaspard de Prony, the man who headed the project, claimed that he could ‘manufacture logarithms as easily as one manufactures pins’. He had a staff of nearly 90 human calculators, many of whom were former servants or wig dressers whose pre-revolutionary skills had become redundant (if not treasonous) in the new regime. Most of the calculations were finished by 1796, but by then the government had lost interest, and de Prony’s gigantic manuscript was never published. Today it is housed in the Paris Observatory.
Briggs’s and Vlacq’s tables remained the basis for all log tables for 300 years, until the Englishman Alexander J. Thompson in 1924 began work manually on a new set accurate to 20 places. Yet instead of giving an old concept a modern sheen, Thompson’s work was already outdated when he finished it, in 1949. By then computers could generate the tables easily.
When you plot the digits 1 to 10 on a ruler positioned to their log values, you get the following pattern:

We can carry on like this, say, up to 100.

This is what is known as a logarithmic scale. In the scale, numbers get progressively closer together the higher they are.
Some scales of measurement are logarithmic, which means that for every unit you go up on the scale, it represents a tenfold change in what it is measuring. (In the second scale above, the distance between 1 and 10 is equal to the distance between 10 and 100.) The Richter scale, for example, which measures the amplitude of waves recorded by seismographs, is the most commonly used logarithmic scale. An earthquake that registers 7 on the Richter scale triggers an amplitude that is ten times more than an earthquake that registers a 6.
In 1620 the English mathematician Edmund Gunter was the first person to mark the logarithmic scale on a ruler. He noticed that he could multiply by adding lengths of this ruler. If a compass was placed with the left spike at 1, and the right at
a
, then when the left spike was moved to
b
, the right spike pointed to
a
×
b
. The diagram below shows the compass set to 2 and then positioned with the left spike at 3, putting the right spike at 2×3 = 6.
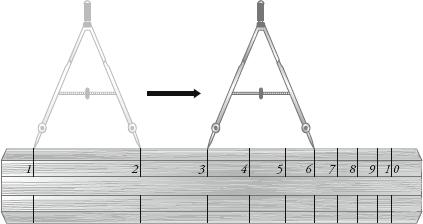
Gunter multiplication.
Not long afterwards William Oughtred, an Anglican minister, improved on Gunter’s idea. He dispensed with the compasses, instead placing two wooden log scales next to each other to create a device known as the slide-rule. Oughtred devised two styles of slide-rule. One version used two straight rulers and the other used a circular disc with two cursors. But Oughtred, for unknown reasons, didn’t publish news of his invention. In 1630, however, one of his students, Richard Delamain, did. Oughtred was outraged, accusing Delamain of being a ‘pickpurse’, and the feud over the slide-rule’s origins continued until Delamain’s death. ‘This scandall,’ complained Oughtred at the end of his life, ‘hath wrought me much prejudice and disadvantage.’
The slide-rule was a calculating machine of fantastic ingenuity, and while it may now be obsolete it still has fanatical devotees. I visited one of them, Peter Hopp, in Braintree, Essex. ‘Between the 1700s and 1975 every single technological innovation was invented using a slide-rule,’ he told me when he picked me up at the station. Hopp, a retired electrical engineer, is an extremely affable man with wispy eyebrows, blue eyes, and luxurious jowls. He was taking me to see his slide-rule collection, one of the world’s largest, which contains more than a thousand of these forgotten heroes of our scientific heritage. On the drive to his home we chatted about collecting. Hopp said the best stuff was auctioned directly on the internet, where competition inevitably pushed prices higher. A rare slide-rule, he said, can easily cost hundreds of pounds.
When we arrived at his house, his wife made us a cup of tea and we retired to his study, where he presented me with a wooden 1970s Faber-Castell slide-rule with a magnolia-coloured plastic finish. The rule was the size of a normal 30cm ruler and had a sliding middle section. On it, several different scales were marked in tiny writing. It also had a transparent movable cursor marked with a hairline. The shape and feel of the Faber-Castell were deeply evocative of a kind of post-war, pre-computer-age nerdiness – when geeks had shirts, ties and pocket protectors rather than T-shirts, sneakers and iPods.
I went to secondary school in the 1980s, by which time slide-rules were no longer used, so Hopp gave me a quick tutorial. He recommended that as a beginner I should use the log scale from 1 to 100 on the main ruler and adjacent log scale from 1 to 100 on the sliding middle section.
Multiplication of two numbers using a slide-rule – which also used to be called a slipstick in the US – is performed by lining up the first number marked out on one scale with the second number marked out on the other scale. You don’t even need to understand what logs are – you just need to slide the middle ruler to the correct position and read the scale.
For example, say I want to multiply 4.5 by 6.2. I need to add the length that is 4.5 on one ruler to the length that is 6.2 on the other. This is done by sliding the 1 on the middle ruler to the point where 4.5 is on the main ruler. The answer to the multiplication is the point on the main ruler adjacent to where 6.2 is on the middle ruler. The diagram below makes this clear:
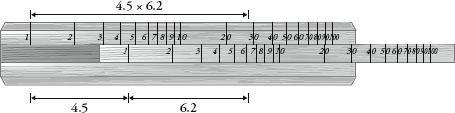
How to multiply with a slide-rule.
Using the hairline cursor, it is easy to see where one scale meets the other. Moving up from 6.2 on the middle ruler, I can see that it crosses the main ruler at
just under
28, which is a correct answer. Slide-rules are not precise machines. Or rather, we are imprecise in our use of them. In reading a slide-rule, we are estimating where a number is on an analogue scale, rather than finding a clear result. Yet despite their inherent imprecision, Hopp said that – for his purposes as an engineer, at least – slide-rules were accurate enough for most uses.
The log scale on the slide-rule I used went from 1 to 100. There are also scales that go from 1 to 10, which are used for greater accuracy because there is more space between the numbers. For this reason, whenever you use a slide-rule it’s always best to convert the original sum into numbers between 1 and 10 by moving the decimal point. For example, in order to multiply 4576 by 6231, I would turn this into the multiplication of 4.576 by 6.231. Once I have the answer, I will move the decimal point six places back to the right. When I put in 4.576 and line it up with 6.231 I get around 28.5, meaning that the answer to 4576×6231 is about 28,500,000. The precise answer, as calculated above, using logs, is 28,513,056. Not a bad estimate. Usually, a slide-rule like the Faber-Castell will give you accuracy to three significant figures – which is often all that is required. What I lost in accuracy, however, I gained in speed – this sum took me under five seconds to do. Using log tables would have taken me ten times longer.