Alex’s Adventures in Numberland (16 page)

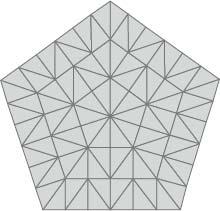
Nonperiodic tessellation.

Many types of tile that can be arranged periodically can also be arranged nonperiodically. The question that tantalized mathematicians in the second half of the twentieth century, however, was whether or not there existed any sets of tiles that could be tiled
only
nonperiodically. These would be tiles that could cover a plane surface but were incapable of producing repeated patterns. The idea is counter-intuitive – if tiles are so well suited and harmonious that they can tile a plane without leaving any gaps, then it would seem natural that they are able to do so in a regular, repeating way. For a long time it was believed that nonperiodic tiles did not exist.

Then along came Roger Penrose with his kites and darts. In the 1970s, Penrose – a cosmologist – thrilled the maths world when he developed several types of nonperiodic tiles. The simplest were created by judiciously cutting a rhombus in two, to form two different shapes, which he called a kite and a dart. Since any four-sided shape can produce a periodic tessellation, Penrose then had to formulate a rule for how these tiles could be joined that would restrict the patterns they could make to being nonperiodic. He did this by drawing two arcs on each kite and dart and stipulating that tiles must be connected so that like arc always joins with like.

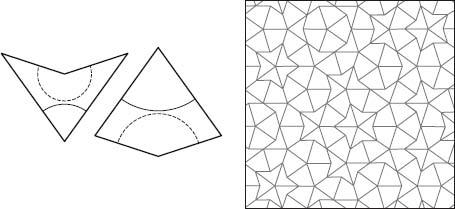
Penrose’s dart and kite can tile only nonperiodically.

The discovery of nonperiodic tiling was an exciting breakthrough for maths, but not as exciting as it would later be for physics and chemistry. In the 1980s researchers were amazed to discover a type of crystal that they did not believe existed. The tiny structure displayed a nonperiodic pattern, behaving in three dimensions just like Penrose’s tiles did in two. The existence of these structures – called quasicrystals – changed the way scientists understood the nature of matter, since it contradicted classical theory that all crystals must have symmetrical lattices derived from the Platonic solids. Penrose may have invented his tiles for fun, but they were unduly prophetic about the natural world.

Half a millennium ago, Islamic geometers might also have understood about non-periodic tessellations. In 2007 Peter J. Lu from Harvard University and Paul J. Steinhardt from Princeton claimed that their studies of mosaics in Uzbekistan, Afghanistan, Iran, Iraq and Turkey showed that the craftsmen had made ‘nearly perfect quasi-crystalline Penrose patterns, five centuries before discovery in the West’. It is possible, therefore, that Islamic mathematics may have been even more advanced than historians of science have traditionally thought.

Hinduism also used geometry to illustrate the divine. Mandalas are symbolic representations of deities and the cosmos. The most complex of these is the Sri Yantra, a figure made up of five triangles pointing down and four pointing up, all overlapping a central point, or
bindu
. It is said to represent the essential outline of the universal processes of emanation and reabsorption, and is used as a focus for meditation and worship. Constructing it is very imprecise – its structure is enigmatically described in a long poem, but the sacred texts do not give enough detail. Mathematicians are baffled to this day by exactly how it is properly constructed.

Another Eastern culture has long embraced the joys of geometric shapes. Origami, the art of paper-folding, evolved from the custom of Japanese farmers thanking the gods at harvest time by making an offering of some of their crops on a piece of paper. Rather than placing the produce on a flat sheet, they would make one diagonal fold in the paper to give the offering a human touch. Origami flourished in Japan over the last few hundred years as an informal pastime, the kind of thing parents did with their children for fun. It fitted in perfectly with the Japanese love of artistic understatement, attention to detail and economy of form.

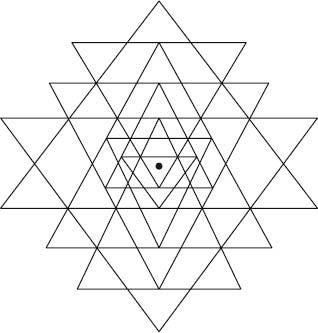
The Sri Yantra.

Business-card origami sounds like the ultimate Japanese invention, uniting two national passions. In fact, the practice is abhorrent to them. The Japanese see business cards as an extension of the individual, so playing with them is considered grossly offensive, even with origamic intent. When I tried to fold one in a Tokyo restaurant I was almost ejected for my antisocial behaviour. In the rest of the world, however, business-card origami is a modern paper-folding subgenre. It dates back more than a hundred years, to the (now obsolete) practice of visiting-card origami.

A simple example is to fold a business card so that the bottom right corner meets the top left corner, and then fold the overlaps, as shown overleaf. Repeat this with another business card, except this time fold the bottom left to the top right. You now have two pieces that can be slotted together to form a tetrahedron. It is a winning way, so I am told, to hand over your business card during mathematics conferences.

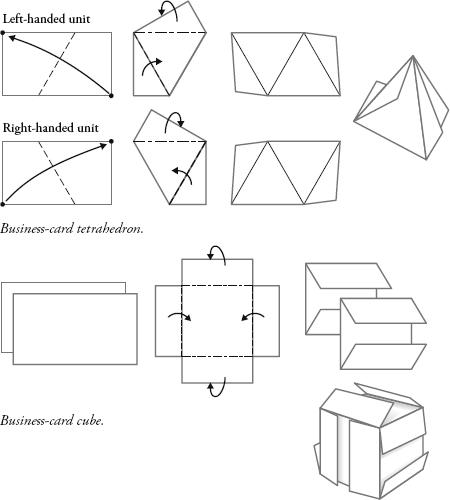
The octahedron can be made from four cards, and an icosahedron with ten of them. It is also easy to make a fourth Platonic solid – the cube. Put two cards on top of each other like a plus sign and fold the flaps as shown above. This creates the shape of a square. Six cards folded in this way slot together to form a cube, although the flaps are on the outside. You need another six cards to slide on to each face in order to make the cube clean.

The Zen master of business-card origami is Jeannine Mosely, a software developer from Massachussetts. A few years ago she found herself with 100,000 cards in her garage – she inherited three batches from her colleagues at work, the first time when the company changed its name, the second when the company moved addresses, and then again when it was discovered that the new cards all had a typo. You can make a lot of tetrahedrons with 100,000 business cards. Yet Mosely had much grander ambitions than the Platonic solids. Why limit herself to the ancient Greeks? Had 2000 years of geometry not produced a more exciting 3-D shape? With her resources Mosely felt ready to tackle the ultimate challenge of her art, the Menger sponge.

Before we get to the Menger sponge, I need to introduce the Sierpinski carpet. The bizarre shape was invented by the Polish mathematician Waclaw Sierpinski in 1916. You start with a black square. Imagine it is made of nine identical subsquares, and remove the central one (figure A). Now for each of the remaining subsquares, repeat the operation – that is, imagine they are made of nine subsquares and remove the central one (B). Repeat this process again (C). The Sierpinski carpet is what you get if you continue this process ad infinitum.

In 1926 the Austrian mathematician Karl Menger came up with the idea of a three-dimensional version of the Sierpinski carpet, which is now known as the Menger sponge. You start with a cube. Imagine it is made up of 27 identical subcubes and remove the subcube at the very centre, as well as the 6 subcubes that are in the centre of each of the sides of the original cube. You are left with a cube that looks like it has three square holes drilled through it (D). Treat each of the 20 subcubes that are left like the original cube, and extract 7 of the 27 subcubes (E). Repeat the process again (F) and the block starts to look like it has been devoured by a cluster of geometrically obsessed woodworm.

Thinking inside the box: Jeannine Mosely and her Menger Sponge.

The Menger sponge is a brilliantly paradoxical object. As you continue the iterations of taking out smaller and smaller cubes the volume of the sponge gets smaller and smaller, eventually becoming invisible – as though the woodworm have eaten the whole lot. Yet each iteration of cube removal also makes the surface area of the sponge increase. By taking more and more iterations you can make the surface area larger than any area you want, meaning that as the number of iterations approaches infinity, the surface area of the sponge also approaches infinity. In the limit, the Menger sponge is an object with an infinitely large surface area that is also invisible.

Mosely constructed a level-three Menger sponge – in other words, a sponge after three iterations of cube removal (F). The project took her ten years. She enlisted the help of abut 200 people, and used 66,048 cards. The finished sponge was 4ft 8in high, wide and deep.