Alex’s Adventures in Numberland (15 page)

Using Euclid’s method, many mathematicians after him have asked new questions and made new discoveries. For example, in 1471 the German mathematician Regiomontanus wrote a letter to a friend in which he posed the following problem: ‘At what point on the ground does a perpendicularly suspended rod appear largest?’ This has been rephrased as the ‘statue problem’. Imagine there is a statue on a plinth in front of you. When you are too close you have to crick your neck and you have a very narrow angle to look up at it. When you are far away, you have to strain your eyes and, again, see it through a very narrow angle. Where, then, is the best place to view it?

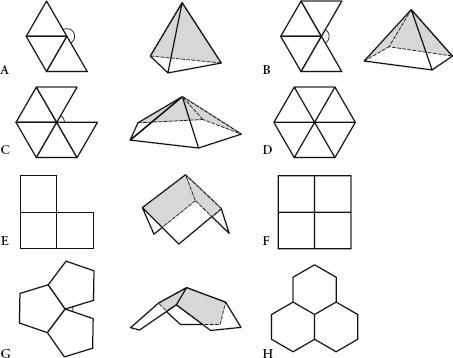
Proof that there are only five Platonic solids.

Consider a side-on view of the situation, as in the diagram opposite. We want to find the point on the dotted line, which represents eye level, such that the angle from the point to the statue is greatest. The solution follows from the third book of
The Elements
, on circles. The angle is largest when a circle that goes through the top and bottom of the statue rests on the dotted line.

The problem is equivalent to that faced by rugby players wanting to know the best distance from the tryline to kick a conversion. If you are too near the opposing tryline the angle is too tight, but if you are too far the angle is also reduced. Where is the optimum position? Here we need to take an aerial view of the pitch and draw a similar diagram. The point on the dotted line of allowed kick spots that subtends the greatest angle to the posts is precisely the point touched by a circle that passes through both posts and rests on the line.

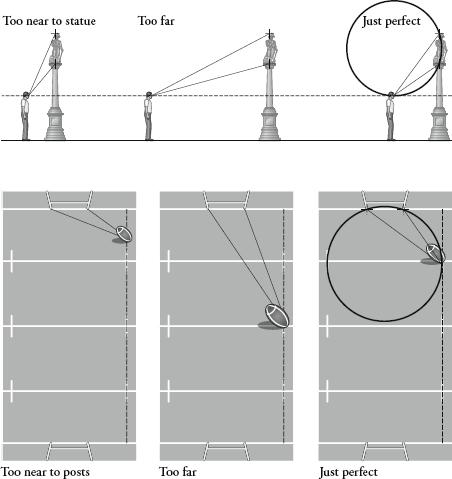
Regiomontanus’s statue and rugby problem.

Perhaps the most stunning result in Euclidean geometry, though, is one that reveals an astonishing property about triangles. Let’s first consider where the centre of a triangle is. This is a surprisingly unclear issue. In fact, there are four ways we can define the centre of a triangle and they all represent different points (unless the triangle is equilateral, when they all coincide). The first is called the
orthocentre
, and is the intersection of the lines from each vertex that meet the opposing sides perpendicularly, which are called the
altitudes
. It is already pretty amazing to think that, for any triangle, the altitudes always meet at the same point.

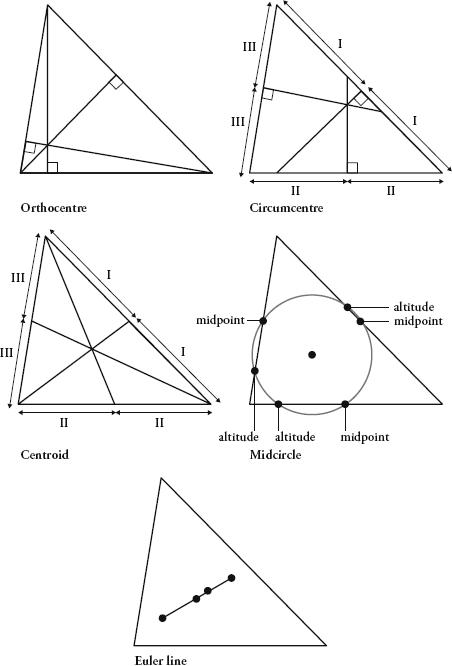
Construction of the Euler line.

The second is the
circumcentre
, which is the intersection of the perpendiculars drawn from the halfway points of the sides. Again, it is very neat that these lines will also always meet, whatever triangle you choose.

The third is the
centroid
, which is the intersection of the lines that go from the vertex to the midpoints of opposing lines. They always meet too. Finally, the
midcircle
is a circle that passes through the midpoints of each side and also the intersections of the sides and the altitudes. Every triangle has a midcircle, and its centre is the fourth type of middle point a triangle can have.

In 1767 Leonhard Euler proved that for all triangles the orthocentre, the circumcentre, the centroid and the centre of the midcircle are always on the same line. This is mind-blowing. Whatever the shape of a triangle these four points have a dazzlingly uniform relation to each other. The harmony is truly wondrous. Pythagoras would have been most awed.

Though this may be hard to fathom these days,
The Elements
was a literary sensation. Until the twentieth century, it is said to have had more editions printed than any other book except the Bible. This was all the more remarkable since
The Elements
is no easy read. One edition, however, is worth mentioning for its unorthodox approach in making the text accessible. Oliver Byrne, whose day job was Surveyor of Her Majesty’s Settlements in the Falkland Islands, rewrote Euclid in colour. Instead of the long proofs, he drew illustrations in which angles, lines and areas were marked in geometrical blocks of red, yellow, blue or black. His
Elements…in which coloured diagrams and symbols are used instead of letters for the greater ease of learning
was published in 1847 and has been described as ‘one of the oddest and most beautiful books of the whole nineteenth century’. In 1851 it was one of the few British books on display at the Great Exhibition, though the public failed to see the excitement. Indeed, Byrne’s publishers went bust in 1853, with more than 75 percent of stock of
The Elements
unsold. Its high production costs had contributed to the bankruptcy.

Byrne’s illustrated proofs did make Euclid more intuitive, predating colour-coordinated textbooks of recent years. Aesthetically it was also ahead of its time. The gaudy primary colours, asymmetrical layout, angularity, abstract shapes and plentiful empty space anticipated the paintings of many twentieth-century artists. Byrne’s book looks like a tribute to Piet Mondrian, published 25 years before Mondrian was even born.

As masterful as the Euclidean method was, it could not solve all problems; some quite simple ones, in fact, are unsolvable using just a compass and ruler. The Greeks suffered for this. In 430 bc Athens was struck by a plague of typhoid. Its citizens consulted the oracle at Delos, who advised them to double the size of Apollo’s altar, which was cube-shaped. Relieved that such an apparey easy task would save them, they constructed a new altar where the sides of the cube were double the length of those of the original altar. Yet by doubling the side of a cube, the volume of the cube increases by two cubed, or eight. Apollo was not happy and made the pestilence worse. The challenge that the god set – that is, given a cube, construct a second cube that has twice the volume – is called the Delian Problem, and it is one of the three classic problems of antiquity that cannot be solved by Euclidean tools. The other two are
the squaring of the circle
, which is the construction of a square that has the same area as a given circle, and
the trisection of an angle
, which is the construction of an angle that is a third of a given angle. Realizing why Euclidean geometry cannot solve these problems – and why other methods can – has been a long-time preoccupation of mathematics.

The Greeks were not the only people intrigued by the wonders of geometrical shapes. The most sacred object in Islam is a Platonic solid: the Ka’ba, or Cube, is the black palladium at the centre of Mecca’s Sacred Mosque, around which pilgrims walk anticlockwise during the Hajj. (In fact, its dimensions make it just off a perfect cube.) The Ka’ba also marks the point that worshippers must face during daily prayer, wherever they are in the world. Mathematics plays more of a role in Islam than in any other major religion. More than a millennium before the advent of GPS technology, the requirement to face Mecca relied on complicated astronomical calculations – which is one reason why Islamic science was unequalled for almost a thousand years.

Islamic art is epitomized by the ingenious geometrical mosaic arrangements on the walls, ceilings and floors of its sacred buildings, a consequence of the ban on images of people and animals in holy sites. Geometry was thought to express truth beyond what was merely human, much in keeping with the Pythagorean position that the universe reveals itself through mathematics. The symmetries and endless loops that Islamic craftsmen created in their patterns were an allegory of the Infinite, an expression of the sacred, mathematical order of the world.

The beauty of a repeating mosaic pattern lies not so much in the aesthetic appeal of the replicated image as in the effortlessness with which the tiles perfectly fill the space. The better the geometry, the better the art. Working out what shapes will tile a wall so that there are no gaps and no overlaps is quite a mathematical challenge, familiar to anyone who has ever tiled a bathroom floor. It turns out that only three of the regular polygons are able to ‘tessellate’, which is the technical word for covering a plane so that no region is uncovered. These are the equilateral triangle, the square and the hexagon. In fact, a triangle is not required to be equilateral in order to tessellate. The sides can be of any size. For any triangle, all you need to do is join it to an identical triangle placed upside-down, as in the diagram below. The combined shape is a parallelogram. The parallelogram can be joined with identical ones to form a row, and these rows can fit together side by side. This type of tessellation – in which the same pattern repeats endlessly – is called periodic.

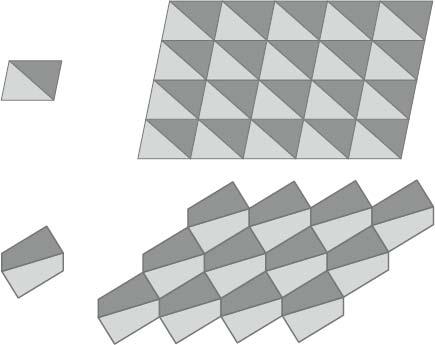
Triangle and quadrilateral tessellations.

A square tile will fill a flat surface. That’s obvious. So does any rectangle. That is also a trivial observation – staring at a brick wall is equally the scrutiny of a at’ion of rectangles. What is surprising, however, is that any shape with four sides can also produce periodic tessellations. Draw any four-sided shape. Join this shape with one upside-down, as we did with the triangle above, and you create a six-sided shape, an irregular hexagon, with the property that each of the opposite edges are equal. Since the opposite edges are equal, the shape can be laid in a row such that the edges fit perfectly alongside each other. As the diagram on the previous page shows, this fit works in the direction of each of the sides, and the repeated hexagons cover a plane perfectly.

I said that a periodic tessellation is one that repeats endlessly. There is a more practical definition of periodicity. Imagine a plane extending infinitely in all directions and covered with the triangle tessellation on the previous page. Now imagine making an identical copy of the tessellation on tracing paper and placing it on the plane. Periodicity can be defined as the capacity to lift up the copy, move it along to another position and then to put it back down on the plane so that the pattern of the copy lines up perfectly with the original pattern. We can do this with the triangle tessellation because we can move the copy to the left (or right, or up, or down) by any number of triangles. When the copy is aligned to its new position, the copy is a perfect fit for the tessellation underneath. This definition of periodicity is helpful because it is now easier to explain the concept of
nonperiodicity
. A nonperiodic tessellation is one that when a copy is made, there is only one position where the copy fits perfectly over the plane – the original position. For example, the tessellation below opposite is nonperiodic. (Imagine that the tessellation goes on for ever, in widening concentric pentagons.) If you made a copy of it, the copy coincides only with the underlying tessellation in one position.