Alex’s Adventures in Numberland (10 page)

This way of ordering is known as the Fu Hsi sequence. (Strictly speaking, it is the inverse of Fu Hsi, but they are mathematically equivalent.) When Leibniz was made aware of the binary nature of Fu Hsi, it gave him ‘a high opinion of [the
I Ching
’s] profundity’. Since he thought that the binary system mirrored Creation, his discovery that it also underlay Taoist wisdom meant that Eastern mysticism could now be accommodated within his own Western beliefs. ‘The substance of the ancient theology of the Chinese is intact and, purged of additional errors, can be harnessed to the great truths of the Christian religion,’ he wrote.

Part of the Fu Hsi sequence of the
I Ching
and its binary equivalent.

Leibniz’s panegyrics on base two were a rather eccentric preoccupation of the pre-eminent polymath of his day. Yet in ascribing a fundamental importance to the system, he was more prescient than even he could ever have imagined. The digital age runs on binary, as computer technology relies at a most basic level on a language comprised of 0s and 1s. ‘Alas!’ wrote mathematician Tobias Dantzig. ‘What was once hailed as a monument to monotheism ended in the bowels of a robot.’

‘Freedom is the freedom to say two plus two equals four,’ wrote Winston Smith, the protagonist of George Orwell’s
Nineteen Eighty-Four
. Orwell was making a comment not only about freedom of speech in the Soviet Union, but also about mathematics. Two plus two is always four. No one can tell you it isn’t. Mathematical truths cannot be influenced by culture or ideology.

On the other hand, our approach to mathematics is very much influenced by culture. The selection of base ten, for example, was not premised on mathematical reasons but on physiological ones, the number of our fingers and toes. Language also shapes mathematical understanding in surprising ways. In the West, for example, we are held back by the words we have chosen to express numbers.

In almost all Western European languages, number words do not follow a regular pattern. In English we say twenty-one, twenty-two, twenty-three. But we don’t say tenty-one, tenty-two, tenty-three – we say eleven, twelve, thirteen. Eleven and twelve are unique constructions, and even though thirteen is a combination of three and ten, the three part comes before the ten part – unlike twenty-three, when the three part comes after the twenty part. Between ten and twenty, English is a mess.

In Chinese, Japanese and Korean, however, number words do follow a regular pattern. Eleven is written ten one. Twelve is ten two, and so on with ten three, ten four up to ten nine for nineteen. Twenty is two ten, and twenty-one is two ten one. You pronounce numbers in all cases just as you see them written down. So what? Well, it does make a difference at a young age. Experiments have repeatedly shown that Asian children find it easier to learn to count than Europeans. In one study with Chinese and American four-and five-year-olds, the two nationalities performed similarly when learning to count to 12, but the Chinese were about a year ahead with higher numbers. A regular system also makes arithmetic clearer to understand. A simple sum such as twenty-five plus thirty-two when expressed as two ten five plus three ten two is one step closer to the answer already: five ten seven.

Not all European languages are irregular. Welsh, for example, is just like Chinese. Eleven in Welsh is
un deg un
(one ten one); twelve is
un deg dau
(one ten two), and so on. Ann Dowker and Delyth Lloyd at the University of Oxford tested the maths abilities of Welsh-and English-speaking kids from the same Welsh village. While Asian children may be better than American children because of many cultural factors, such as hours spent practising or attitudes towards maths, cultural factors can be eliminated if the children are all living in the same place. Dowker and Lloyd concluded that while general arithmetic performance was more or less equal between Welsh-and English-speakers, the Welsh-speakers did demonstrate better mathematical skills in specific areas – such as reading, comparing and manipulating two-digit numbers.

German is even more irregular than English. In German, twenty-one is
einundzwanzig
, or one-and-twenty, twenty-two is
zweiundzwanzig
, or two-and-twenty, and this continues with the unit value preceding the tens value all the way up to 99. This means that when a German says a number over 100, the digits are not pronounced in a consecutive order: three hundred and forty-five is
dreihundertfünfundvierzig
, or three-hundred-five-and-forty, which lists the numbers in the higgledy-piggledy form 3-5-4. Such is the level of concern in Germany that this makes numbers more confusing than they have to be, that a campaign group
Zwanzigeins
(Twenty-one) has been set up to push for a change to a more regular system.

And it’s not just the positioning of number words, or their irregular forms between eleven and nineteen, that puts the speakers of the main Western European languages at a disadvantage with some Asian language-speakers. We are also handicapped by how long it takes us to say numbers. In
The Number Sense
yi, er, san, si, wu, liu, qi, ba, jiu
. They can be uttered in less than a quarter of a second, so in a two-second span a Chinese-speaker can rattle through nine of them. English number words, by contrast, take just under a third of a second to say (thanks to the frankly cumbersome ‘seven’, with two syllables, and the extended syllable ‘three’), so our limit in two seconds is seven. The record, however, goes to the Cantonese, whose digits are spoken with even more brevity. They can remember ten of them in a two-second period.

While Western languages seem to be working against any mathematical ease of understanding, in Japan language is recruited as an ally. Words and phrases are modified in order to make their multiplication tables, called
kuku
, easier to learn. The tradition of these tables originated in ancient China, spreading to Japan around the eighth century.
Ku
in Japanese is nine, and the name comes from the fact that the tables used to begin at the end, with 9×9 = 81. Around 400 years ago they were changed so that the
kuku
now begins ‘one one is one’.

The words of the
kuku
are simply:

This carries on to ‘One nine is nine’, and then the twos begin with:

And so on to nine nine is eighty-one.

So far, this seems very similar to the plain British style of reciting the times tables. In the
kuku
, however, whenever there are two ways to pronounce a word, the way that flows better is used. For example, the word for one can be
in
or
ichi
, and rather than starting the
kuku
with either
in in
or
ichi ichi
, the more sonorous combination
in ichi
is used. The word for eight is
ha
. Eight eights should be
ha ha
. Yet the line in the
kuku
for 8×8 is
happa
since it rolls quicker off the tongue. The result is that the
kuku
is rather like a piece of poetry, or a nursery rhyme. When I visited an elementary school in Tokyo and watched a class of seven-and eight-year-olds practise their
kuku
, I was struck by how much it sounded like a rap – the phrases were syncopated and jolly. Certainly it bore no relation to how I remember reciting my times tables at school, which was with the metronomic delivery of a steam train going up a hill. Makiko Kondo, the teacher, said that she teaches her pupils
kuku
with an uptempo rhythm because it makes it fun to learn. ‘First we get them to recite it, and only some time later do they come to understand the real meaning.’ The of the
kuku
seems to embed the times tables in Japanese brains. Adults told me that they know, for example, that seven times seven is 49 not because they remember the maths but because the music of ‘seven seven forty-nine’ sounds right.

While the irregularities of Western number words may be unfortunate for budding arithmeticians, they are of extreme interest to mathematical historians. The French for eighty is
quatre-vingts
, or four-twenties, indicating that ancestors of the French once used a base-20 system. It has also been suggested that the reason why the words for ‘nine’ and ‘new’ are identical or similar in many Indo-European languages, including French (
neuf, neuf
), Spanish (
nueve, nuevo
), German (
neun, neu
) and Norwegian (
ni, ny
) is a legacy of a long-forgotten base-eight system, where the ninth unit would be the first of a new set of eight. (Excluding thumbs, we have eight fingers, which could be how such a base developed. Or possibly from counting the gaps between the fingers.) Number words are also a reminder of how close we are to the numberless tribes of the Amazon and Australia. In English,
thrice
can mean both three times and many times; in French,
trois
is three and
très
is very: shadows, perhaps, of our own ‘one, two, many’ past.

Whereas certain aspects of number – such as the base, the style of numeral or the form of the words used – have differed widely between cultures, the early civilizations were surprisingly unified in the mechanics of how they counted and calculated. The general method they used is called ‘place value’ and is the principle by which different positions are used to represent different orders of number. Let’s consider what this means in the context of shepherds in medieval Lincolnshire. As I wrote earlier, they had 20 numbers from
yan
to
piggot
. Once a shepherd counted 20 sheep, he put a pebble aside and started counting from
yan
to
piggot
all over again. If he had 400 sheep, he would have 20 pebbles, since 20×20 = 400. Now imagine the shepherd had a thousand sheep. If he counted them all he would have 50 pebbles, since 50×20 = 1000. Yet the problem with the shepherd having 50 pebbles is that he has no way to count them, since he cannot count higher than 20!

A way to solve this is to draw parallel furrows on the ground, as in the figure overleaf. When the shepherd counts 20 sheep he puts a pebble in the first furrow. When he counts another 20 sheep, he puts another pebble in the first furrow. Slowly the first furrow fills up with pebbles. When the time comes to put a twentieth pebble in the furrow, however, he instead puts a single pebble in the second furrow, and clears the first furrow of all pebbles. In other words, one pebble in the second furrow means 20 pebbles in the first – just as one pebble in the first furrow means 20 sheep. A pebble in the second row stands for 400 sheep. A shepherd who has a thousand sheep and uses this procedure will have two pebbles in the second furrow, and ten in the first. By using a place-value system like this one – by which each furrow confers a different value to the pebble in it – he has used only 12 pebbles to count 1000 sheep rather than the 50 he would have needed without it.

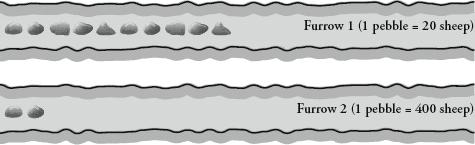
Total sheep = (10
×
20) + (2
×
400)0