Alex’s Adventures in Numberland (8 page)

The most famous dozenalist call-to-arms, though, was an article in
The Atlantic Monthly
in October 1934 by the writer F. Emerson Andrews, which led to the formation of the Duodecimal Society of America, or DSA. (It later changed its name to the Dozenal Society of America since ‘duodecimal’ was deemed to be overly reminiscent of the system they were aiming to replace.) Andrews claimed that base ten had been adopted with ‘inexcusable shortsightedness’ and wondered whether it ‘would be so tremendous a sacrifice’ to abandon it. The DSA initially insisted prospective members pass four tests in dozenal arithmetic, although this requirement was quickly dropped. The
Duodecimal Bulletin
, which continues to this day, is an excellent publication and the only place outside medical literature with articles on hexadactyly, the condition of being born with six fingers. (Which is more common than you might think. About one in every 500 people is born with at least an extra finger or toe.) In 1959 a sister organization, the Dozenal Society of Great Britain, was founded, and a year later the First International Duodecimal Conference was held in France. It was also the last. Still, both societies continue to battle for a dozenal future, seeing themselves as downtrodden militants rallying against the ‘tyranny of ten’.

Michael de Vlieger’s youthful infatuation with base 12 was not a passing phase; he is the current president of the DSA. In fact, he is so committed to the system that he uses it in his job as a designer of digital architectural models.

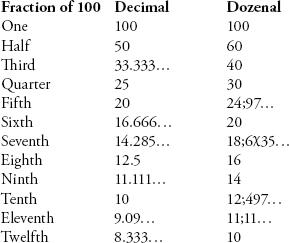
While base 12 certainly makes times tables easier to learn, its greatest advantage is how it cleans up fractions. Base ten is frequently messy when you want to divide. For example, a third of 10 is 3.33…, where the threes go on for ever. A quarter of 10 is 2.5, which needs a decimal place. In base 12, however, a third of 10 is 4 and a quarter of 10 is 3. Nice. Expressed as a percentage, a third becomes 40 percent, and a quarter 30 percent. In fact if you look at how 100 is divided by the numbers 1 to 12, base 12 provides more concise numbers (note that the semi-colons in the right column stand for the ‘dozenal’ point).

It is this increased precision that makes base 12 better suited to Michael’s needs. Even though his clients supply him with dimensions in decimal, he prefers to translate them into dozenal. ‘It gives me more choices when dividing into simple ratios,’ he said.

‘Avoiding [messy] fractions helps ensure things fit. Sometimes, because of time constraints or late-breaking changes, I will need to quickly apply a lot of change at a location that doesn’t jive with the grid I initially set up. Thus it’s important to have predictable simple ratios. I’ve got more and cleaner choices with dozenal, and it’s faster.’ Michael even believes that using base 12 gives his business an edge, comparing it to cyclists and swimmers who shave their legs.

The DSA used to want to replace decimal with dozenal, and its fundamentalist wing still does, but Michael’s ambitions are more modest. He wants simply to show people that there is an alternative to the decimal system, and that perhaps it suits their needs better. He knows that the chances of the world abandoning
dix
for
douze
are non-existent. The change would be both confusing and expensive. And decimal works well enough for most people – especially in the computer age, where mental arithmetic skills are less required generally. ‘I would say that dozenal is the optimum base for general computation, for everyday use,’ he added, ‘but I am not here to convert anybody.’

An immediate goal of the DSA is to get the numerals for dek and el into Unicode, the repertoire of text characters used by most computers. In fact, a major debate in dozenal society is which symbols to use. The DSA standard
and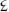
were designed in the 1940s by William Addison Dwiggins, one of the US’s foremost font designers and the creator of Futura, Caledonia and Electra. Isaac Pitman preferred
and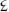
. Jean Essig, a French enthusiast, preferred
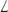and
. Some practical members would prefer * and # since they are already on the 12 buttons of a touch-tone phone. The number words are also an issue. The
Manual of the Dozen System
(written in 1960, or 1174 in dozenal) recommends the terms dek, el and do (with gro for 100, mo for 1000, and do-mo, gro-mo, bi-mo and tri-mo for the next highest powers of do). Another suggestion is to keep ten, eleven and twelve and continue with twel-one, twel-two, and so on. Such is the sensitivity over terminology that the DSA is careful not to push any system. Great care is needed not to marginalize devotees of any particular symbol or term.

Michael’s love of avant-garde bases did not stop at 12. He has toyed with eight, which he sometimes uses when doing DIY at home. ‘I use bases as tools,’ he said. And he has gone up to base 60. For this he had to design 50 extra symbols to add to the ten digits we have already. His purpose was not practical. He described working in base 60 as like going up a high mountain. ‘I can’t live up there. It is too big a grouping. In the valley it is decimal, and there I can breathe. But I can visit the mountain to see what the view is like.’ He has written out tables of factors in a base 60, or sexagesimal, system, and stared in wonder at the patterns they revealed. ‘There definitely is a beauty there,’ he told me.

While base 60 seems like the product of an extraordinarily fertile imagination, sexagesimal has historical pedigree. It is actually the most ancient base system that we know of.

The simplest form of numerical notation is the tally. It has been used in different forms across the world. The Incas kept count by tying knots on ropes, while cave dwellers painted marks on rocks and, since the invention of wooden furniture, bedposts have – figuratively, at least – been marked with notches. The oldest discovered ‘mathematical artefact’ is believed to be a tally stick: a 35,000-year-old baboon fibula found in a Swaziland cave. The ‘Lebombo bone217; has 29 lines scraped on it, which possibly denote a lunar cycle.

As we saw in the previous chapter, humans can instantly tell the difference between one item and two, between two items and three, but beyond four it gets difficult. This is true of notches as well. For any convenient system of tally-keeping, the tallies need to be grouped. In Britain, tally convention is to mark four vertical lines and then make the fifth a diagonal crossing through them – the so-called ‘five-bar gate’. In South America, the preferred style is for the first four lines to mark a square and the fifth is a diagonal in the square. The Japanese, Chinese and Koreans use a more elaborate method, constructing the character, which means ‘correct’ or ‘proper’. (The next time you have sushi, ask the waiter to show you how he is tallying your dishes.)