Alex’s Adventures in Numberland (4 page)
Read Alex’s Adventures in Numberland Online
Authors: Alex Bellos

In Karen Wynn’s experiment, babies were tested on their ability to distinguish the correct number of dolls behind a screen.
The Swiss psychologist Jean Piaget (1896–1980) argued that babies build up an understanding of numbers slowly, through experience, so there was no point in teaching aithmetic to children younger than six or seven. This influenced generations of educators, who often preferred to let primary-age pupils play around with blocks in lessons rather than introduce them to formal mathematics. Now Piaget’s views are considered outdated. Pupils come face to face with Arabic numerals and sums as soon as they get to school.
Dot experiments are also the cornerstone of research into adult numerical cognition. A classic experiment is to show a person dots on a screen and ask how many dots he or she sees. When there are one, two or three dots, the response comes almost instantly. When there are four dots, the response is significantly slower, and with five slower still.
So what! you might say. Well, this probably explains why in several cultures the numerals for 1, 2 and 3 have been one, two and three lines, while the number for 4 is
not
four lines. When there are three lines or fewer we can tell the number of lines straight away, but when there are four of them our brain has to work too hard and a different symbol is necessary. The Chinese characters for one to four are ,
, ,
, and
and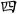 . Ancient Indian numerals were
. Ancient Indian numerals were ,
, ,
, and
and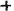 . (If you join the lines, you can see how they turned into the modern 1, 2, 3 and 4.)
. (If you join the lines, you can see how they turned into the modern 1, 2, 3 and 4.)
In fact, there is some debate about whether the limit of the number of lines we can grasp instantly is three or four. The Romans actually had the alternatives IIII and IV for four. The IV is much more instantly recognizable, but clock faces – perhaps for aesthetic reasons – tended to use the IIII. Certainly, the number of lines, dots, or sabre-toothed tigers that we can enumerate rapidly, confidently and accurately is no more than four. While we have an
exact
sense of 1, 2 and 3, beyond 4 our exact sense wanes and our judgements about numbers become
approximate
. For example, try to guess quickly how many dots are at the top of the page opposite.

It’s impossible. (Unless you are an autistic savant, like the character played by Dustin Hoffman in
Rain Man
, who would be able to grunt in a split second ‘Seventy-five’.) Our only strategy is to estimate, and we’d probably be far off the mark.
Researchers have tested the extent of our intuition of amounts by showing volunteers images of different numbers of dots and asking which set is larger, and our proficiency at discriminating dots, it turns out, follows regular patterns. It is easier, for example, to tell the difference between a group of 80 dots and a group of 100 dots than it is between two groups of 81 and 82 dots. Similarly, it is easier to discriminate between 20 and 40 dots than it is between 80 and 100 dots. In both A and B below, the left set of dots is larger than the right set of dots, yet the length of time it takes us to process the information is noticeably longer in case B.

Scientists have been surprised by how strictly our powers of comparison follow mathematical laws, such as the multiplicative principlsti his book
The Number Sense
, the French cognitive scientist Stanislas Dehaene gives the example of a person who can discriminate 10 dots from 13 dots with an accuracy of 90 percent. If the first set is doubled to 20 dots, how many dots does the second set need to include so that this person still has 90 percent accuracy in discrimination? The answer is 26,
exactly double
the original number of the second set.
Animals are also able to compare sets of dots. While they do not score as highly as we do, the same mathematical laws also seem to govern their skills. This is pretty remarkable. Humans are unique in having a wonderfully elaborate system of counting. Our life is filled with numbers. Yet, for all our mathematical talent, when it comes to perceiving and estimating large numbers our brains function just like those of our feathered and furry friends.
Human intuitions about quantities led, over millions of years, to the creation of numbers. It is impossible to know exactly how this happened, but it is reasonable to speculate that it arose from our desire to track things – such as moons, mountains, predators or drum beats. At first we may have used visual symbols, such as our fingers, or notches on wood, in a one-to-one correspondence with the object we were tracking – two notches or two fingers means two mammoths, three notches or three fingers means three, and so on. Later on we will have come up with words to express the concepts of ‘two notches’ or ‘three fingers’.