Alex’s Adventures in Numberland (9 page)

Tally systems of the world.

Around 8000
BC
a practice of using small clay pieces with markings to refer to objects emerged throughout the ancient world. These tokens primarily recorded numbers of things, such as sheep to be bought and sold. Different clay pieces referred to different objects or numbers of objects. From that moment sheep could be counted without actually being there, which made trade and stock-keeping much easier. It was the birth of what we understand now as numbers.

In the fourth millennium bc in Sumer, an area now in present-day Iraq, this token system evolved into a script in which a pointed reed was pressed into soft clay. Numbers were first represented by circles or fingernail shapes. By around 2700 bc the stylus had a flat edge and the imprints looked rather like bird footprints, with different imprints referring to different numbers. The script, called cuneiform, marked the beginning of the long history of Western writing systems. It is wonderfully ironic to think that literature was a by-product of a numerical notation invented by Mesopotamian accountants.

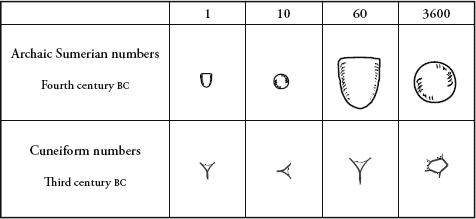
In cuneiform there were symbols only for 1, 10, 60 and 3600, which means the system was a mixture of base 60 and base ten, as the basic set of cuneiform numbers translates into 1, 10, 60 and 60×60. The question why the Sumerians grouped their numbers in sixties has been described as one of the greatest unresolved mysteries in the history of arithmetic. Some have suggested it was the result of the fusion of two previous systems, with bases five and 12, though no conclusive evidence of this has been found.

The Babylonians, who made great advances in maths and astronomy, embraced the Sumerian sexagesimal base, and later the Egyptians, followed by the Greeks, based their time-counting methods on the Babylonian way – which is why, to this day, there are 60 seconds in a minute and 60 minutes in an hour. We are so used to telling the time in base 60 that we never question it, even though it really is quite unexplained. Revolutionary France, however, wanted to iron out what they saw as an inconsistency in the decimal system. When the National Convention introduced the metric system for weights and measures in 1793, it also tried to decimalize time. A decree was signed establishing that every day would be divided into ten hours, each containing 100 minutes, each of which contained 100 seconds. This worked out neatly, making 100,000 seconds in the day – compared to 86,400 (60×60×24) seconds. The revolutionary second was, therefore, a fraction shorter thght="0%e normal second. Decimal time became mandatory in 1794 and watches were produced with the numbers going up to ten. Yet the new system was completely bewildering to the populace and abandoned after little more than six months. An hour with 100 minutes is also not as convenient as an hour with 60 minutes, since 100 does not have as many divisors as 60. You can divide 100 by 2, 4, 5, 10, 20, 25 and 50, but you can divide 60 by 2, 3, 4, 5, 6, 10, 12, 15, 20 and 30. The failure of decimal time was a small victory for dozenal thinking. Not only does 12 divide into 60 but it also divides into 24, the number of hours in a day.

Revolutionary watch with decimal and traditional clock face.

A more recent campaign to decimalize time also flopped. In 1998 the Swiss conglomerate Swatch launched Swatch Internet Time, which divided the day into 1000 parts called beats (equivalent to 1min 26.4secs). The manufacturer sold watches that displayed its ‘revolutionary vision of time’ for a year or so before sheepishly removing them from its catalogue.

The French and Swiss, however, are not the only Western nations to have had barmy counting procedures in the not too distant past. The tally stick, which became outdated the moment the first Sumerian printed his first cuneiform tablet, was used as a form of British currency until 1826. The Bank of England used to issue souped-up tally sticks that were worth a monetary value based on the distance of a mark from the base. A document written in 1186 by the Lord Treasurer Richard Fitzneal set out the values as:

The procedure the Treasury used was, in fact, a system of ‘double tallies’. A piece of wood was split down the middle, giving two parts – the stock and the foil. A value was marked – tallied – on the stock and was also marked on the foil, which acted like a receipt. If I lent some money to the Bank of England, I would be given a stock with a notch indicating the amount – which explains the origin of the words
stockholder
and
stockbroker
– while the bank kept the foil, which had a matching notch.

This practice was abandoned barely two centuries ago. In 1834, the Treasury decided to incinerate the obsolete pieces of wood in a furnace under the Palace of Westminster, the seat of British government. The fire, however, spread out of control. Charles Dickens wrote: ‘The stove, overgorged with these preposterous sticks, set fire to the panelling; the panelling set fire to the House of Commons; the two houses [of government] were reduced to ashes.’ Obscure financial instruments have often impacted on the work of government, but only the tally stick has brought down a parliament. When the palace was rebuilt it had a brand new clock tower, Big Ben, which quickly became the most recognizable landmark in London.

An argument often used in favour of the imperial system over metric is that the words sound better. A case in point is the measures for wine:

This system is base two, or binary, which is usually expressed using the digits 0 and 1. Numbers in binary are the numbers you would use in base ten when only 0 and 1 appear. In other words, the sequence that begins 0, 1, 10, 11, 100, 101, 110, 111, 1000. So, 10 is two, 100 is four, 1000 is eight and so on, with each extra 0 on the end representing multiplication by two. (Which is just like base ten – adding a 0 on the end of a number is multiplication by ten.) In the wine measures, the smallest unit is a gill. Two gills makes a chopin, 4 gills a pint, 8 gills a quart, 16 gills a pottle, etc. The measures replicate perfectly the binary numerals. If a gill is represented by 1, then a chopin is 10, a pint is 100, a quart is 1000 and this carried on all the way to a tun, which is 10,000,000,000,000.

Binary can claim as its cheerleader the greatest mathematician ever to have fallen in love with a non-standard base. Gottfried Leibniz was one of the most important thinkers of the late seventeenth century, a scientist, philosopher and statesman. One of his duties was as librarian to the court of the Duke of Brunswick in Hanover. Leibniz was so excited with base two that he once wrote a letter to the Duke urging him to cast a silver medallion inscribed with the words
Imago Creationis
– ‘in the image of the world’ – as a tribute to the binary system. For Leibniz, binary had practical and spiritual relevance. First, he thought that its capacity for describing every number in terms of doubles facilitated a variety of operations. ‘[It] permits the Assayer to weigh all sorts of masses with few weights and could serve in coinage to give more value with fewer pieces,’ he wrote in 1703. Leibniz did admit that binary had some practical drawbacks. The numbers are much longer when written out: 1000 in decimal, for example, is 1,111,101,000 in binary. But he added: ‘In recompense for its length, [binary] is more fundamental to science and gives new discoveries.’ By looking at the symmetries and patterns in binary notation, he claimed, new mathematical insights are revealed, and number theory is richer and more versatile because of it.

Design for eibniz’s binary medallion, in Johann Bernard Wiedeburg’s
Dissertatio mathematica de praestantia arithmeticae binaria prae decimali
(1718). As well as the words
Imago Creationis
, the Latin reads ‘From nothing comes one and everything, but the one is necessary’.

Second, Leibniz marvelled at how the binary system chimed with his religious views. He believed that the cosmos was composed of being, or substance, and non-being, or nothingness. The duality was perfectly symbolized by the numbers 1 and 0. In the same way that God creates all beings from the void, all numbers can be written in terms of 1s and 0s. Leibniz’s conviction that binary exemplified a fundamental metaphysical truth was – to his great delight – strengthened when later in life he was shown the
I Ching
, the ancient Chinese mystical text. The
I Ching
is a book of divination. It contains 64 different symbols, each of which comes with an accompanying commentary. The reader randomly selects a symbol (traditionally by casting yarrow sticks) and interprets the related text – a little like one might read an astrological chart. Each symbol in the
I Ching
is a hexagram, which means it is composed of six horizontal lines. The lines are either broken or unbroken, corresponding to a
yin
or a
yang
. The 64 hexagrams in the
I Ching
are the full set of combinations of
yins
and
yangs
when taken in groups of six at a time.

A particularly elegant way of ordering the hexagrams is shown opposite. If each
yang
is written 0 and each
yin
is 1, then the sequence matches precisely the binary digits from 0 to 63.