Alex’s Adventures in Numberland (7 page)
Read Alex’s Adventures in Numberland Online
Authors: Alex Bellos

Michael is now 38. I met him in his office, a business suite above some shops in a residential part of St Louis, Missouri. He has thick black hair with a few shoots of white, a round face, dark eyes and sallow skin. His mum is Filipino, while his father is white, and being a mixed-race kid made him the victim of taunts. A clever and sensitive child with an active imagination, he decided to invent his own language so that his classmates couldn’t read his notebooks.
Little Twelvetoes
inspired him to do the same with numbers – and he adopted base 12 for personal use.
Base 12 has 12 digits: 0 to 9 and two extra ones to represent ten and eleven. The standard notation for each of these two ‘transdecimal’ digits is and
and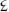 . So, counting to 12 now goes: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9,
. So, counting to 12 now goes: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, ,
,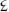 , 10. (See table opposite.)
, 10. (See table opposite.)
The new single digits are given new names to avoid confusion, so is called
is called
dek
and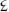 is called
is called
el
. Also, we give 10 the name
do
, pronounced
doh
, and short for dozen, to avoid confusion with 10 in base ten. Counting upwards from
do
in base 12, or ‘dozenal’, we have
do one
for 11,
do two
for 12,
do three
for 13 all the way up to
twodo
for 20.
Michael devised a private calendar using base 12. Each date in this calendar was the number of days, counted in base 12, from the day he was born. He still uses it, and he told me later that I visited him on the 80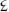 9th day of his life.
9th day of his life.
Michael adopted base 12 for reasons of personal security, but he is not alone in having fallen for its charms. Many seriohinkers have argued that 12 is a better base for a number system because the number is more versatile than 10. In fact, base 12 is more than a number system – it is a politico-mathematical cause. One of its earliest champions was Joshua Jordaine, who in 1687 self-published
Duodecimal Arithmetick
. He claimed that ‘nothing was more natural and genuine’ than counting in twelves. In the nineteenth century high-profile duodeciphiles included Isaac Pitman, who had gained considerable fame for inventing a widespread system of shorthand, and Herbert Spencer, the Victorian social theorist. Spencer urged base-system reform on behalf of ‘working people, people of narrow incomes and the minor shopkeepers who minister to their wants’. The American inventor and engineer John W. Nystrom was also a fan. He described base 12 as ‘duodenal’ – perhaps the most unfortunate double entendre in the history of science.

Dozenal numbers from 1 to 100.
The reason that 12 might be considered superior to ten is because of its divisibility. Twelve can be divided by 2, 3, 4 and 6, whereas ten can be divided only by 2 and 5. Advocates of base 12 argue that we are much more likely to want to divide by 3 or 4 than divide by 5 in our daily lives. Consider a shopkeeper. If you have 12 apples, then you can divide them up into two bags of 6, three bags of 4, four bags of 3, or six bags of 2. This is much more user-friendly than 10, which can only be cleanly divided into two bags of 5, or five of 2. The word ‘grocer’, in fact, is a relic of a retailer’s preference for 12 – it comes from ‘gross’, meaning a dozen dozen, or 144. The multi-divisibility of 12 also explains the utility of imperial measure: a foot, which is 12 inches, can be cleanly divided by 2, 3 and 4 – which is quite a plus for carpenters and tailors.
Divisibility is also relevant to multiplication tables. The easiest tables to learn in any base are the ones of numbers that divide that base. This is why, in base ten, the 2 and 5 times tables – which are just the even numbers and the numbers ending in 5 or 0 – are so painless to recite. Likewise, in base 12 the simplest times tables are also those of its divisors: 2, 3, 4 and 6.

If you look at the final digits of each column, you see a striking pattern. The two times table is, again, all the even numbers. The three times table is all the numbers ending in 3, 6, 9 and 0. The four times table is the numbers ending in 4, 8 and 0, and the six times table all the numbers ending 6 or 0. In other words, in base 12 we get the 2, 3, 4 and 6 times tables for free. Since many children have difficulty in learning their times tables, if we converted to base 12 we would be carrying out a great humanitarian act. Or so the argument goes.
The campaign for base 12 should not be conflated with the crusade against metric by fans of imperial measure. Those people who prefer feet and inches over metres and centimetres have no issue as to whether one foot should be 12 inches, or 10 inches, as it would be in dozenal. Historically, however, an underlying theme of the campaign for base 12 has been a jingoistic anti-Frenchness. Perhaps the finest example of such a view was a pamphlet from 1913 by engineer Rear-Admiral G. Elbrow, in which he called the French metric system ‘retrograde’. He published a list of the dates, in base 12, of the kings and queens of England. He also noticed that Britain had been invaded shortly after each decimal millennium – by the Romans in 43
CE
and the Normans in 1066. ‘What if, at the beginning of the [third millennium],’ he prophesized, ‘these two [countries] may again appear in the same direction, and this time in conjunction?’ Invasion by France and Italy might be averted, he argued, simply by rewriting the year 1913 as 1135, as it would be in dozenal, thus delaying the third millennium by several centuries.