Alex’s Adventures in Numberland (13 page)

Numerology, of course, is now an established dish on the buffet of modern mysticism, with no shortage of gurus willing to advise on lottery numbers or speculate on the portent of a prospective date. It sounds like harmless fun – and I enjoyed my conversation with Jerome Carter immensely – yet giving numbers spiritual significance can also have sinister consequences. In 1987, for example, the military government in Burma issued new banknotes with a face value divisible by nine – for the sole reason that nine was the ruling general’s favourite number. The new notes helped precipitate an economic crisis, which led to an uprising on 8 August 1988 – the eighth of the eighth of ’88. (Eight was the anti-dictatorship movement’s favourite number.) The protest was violently put down, however, on 18 September: in the ninth month, on a day divisible by nine.

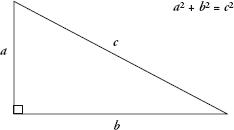
Pythagoras’s Theorem states that
for any right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides
. Its words are imprinted in my brain like an old nursery rhyme or Christmas carol; the phrase is nostalgic and comforting independently of its meaning.

The hypotenuse is the side opposite the right angle, and a right angle is a quarter turn. The theorem is the smash hit of basic geometry, the first truly thought-provoking mathematical concept we are taught at school. What I find exciting about it is how it reveals a deep connection between numbers and space. Not all triangles are right-angled, but when they are, the squares of two of the sides must equal the square of the third. Likewise, the theorem holds in the other direction too. Take any three numbers. If the square of two of them equals the square of the third then you can construct a right-angled triangle out of lengths of those sizes.

In some commentaries about Pythagoras it is said that before he founded the Brotherhood he travelled on a fact-finding mission to Egypt. If he had spent any time on an Egyptian building site he would have seen that the labourers used a trick to create a right angle that was an application of the theorem that would later gain his name. A rope was marked with knots spread out at a distance of 3, 4 and 5 units. Since 3
²
+ 4
²
= 5
²
, when the rope was stretched around three posts, with a knot at each post, it formed a triangle with one right angle.

Pythagoras’s Theorem.

Rope-stretching was the most convenient way to achieve right angles, which were needed so that bricks, or giant stone blocks such as those used to construct the Pyramids, could be stacked next to and on top of each other. (The word hypotenuse comes from the Greek for ‘stretched against’.) The Egyptians could have used many other numbers in addition to 3, 4 and 5 to get real right angles. In fact, there is an infinite number of numbers
a, b
and
c
such that
a2
+
b
²
=
c
²
. They could have marked out their rope into sections of 5, 12 and 13, for example since 25 + 144 = 169, or 8, 15 and 17, since 64 + 225 = 289, or even 2772, 9605 and 9997 (7,683,984 + 92,256,025 = 9940,009) though that would hardly have been practical. The numbers 3, 4, 5 are best suited to the task. As well as being the triple with the lowest value, it is also the only one whose digits are consecutive integers. Due to its rope-stretching heritage, the right-angled triangle with sides that are in the ratio 3:4:5 is known as an Egyptian triangle. It is a pocket-sized right-angle-generating machine that is a jewel of our mathematical patrimony, an intellectual artefact of great power, elegance and concision.

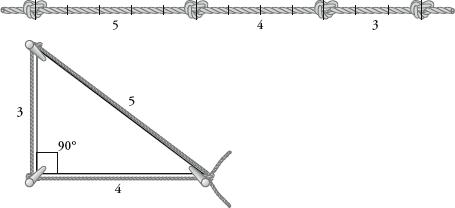
The Egyptian equivalent of a set square was a rope divided in the ratio 3:4:5, which provides a right angle when tied around three posts.

The squares mentioned in Pythagoras’s Theorem can be understood as numbers and also as pictures – literally the squares drawn on the sides of the triangle. Imagine that in the following image the squares are made of gold. You are not engaged to a member of the Pythagorean Brotherhood, so acquiring gold is desirable. Either you can take the two smaller squares, or you can have the one largest square. Which would you prefer?

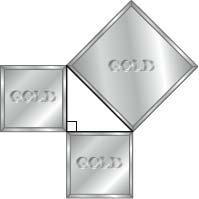
The mathematician Raymond Smullyan said that when he put this question to his students, half the class wanted the big single square and the other half wanted the double. Both sides were stunned when he told them that it would make no difference.

This is true because, as the theorem states, the combined area of the two smaller squares is equal to the area of the large square. All right-angled triangles can be extended in this way to produce three squares such that the area of the large one can be divided exactly into the areas of the two smaller ones. It is not the case that the square on the hypotenuse is sometimes the sum of the squares of the other two sides, and sometimes not. The fit is perfect at all times.

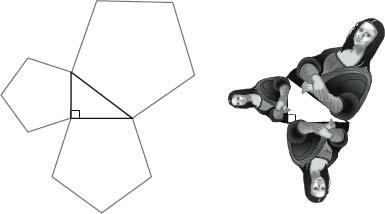
It is not known if Pythagoras really discovered his theorem, even though his name has been attached to it since classical times. Whether or not he did, it vindicates his world-view, demonstrating a remarkable harmony in the mathematical universe. In fact, the theorem reveals a relationship between more than just the squares on the sides of a right-angled triangle. The area of a semicircle on the hypotenuse, for example, is equal to the sum of the areas of the semicircles on the other two sides. A pentagon on the hypotenuse is equal to the sum of pentagons on the other two sides, and this holds for hexagons, octagons and, indeed, any regular or irregular shape. If, say, three Mona Lisas were drawn on a right-angled triangle, then the area of big Mona is equal to the combined area of the two smaller ones.

For me, the real delight in Pythagoras’s Theorem is in the realization of why it must be true. The simplest proof is as follows. It dates back to the Chinese, possibly to before even Pythagoras was born, and is one of the reasons why many doubt he came up with the theorem in the first place.

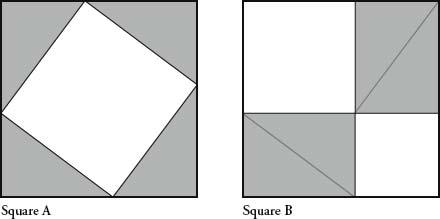
Stare at the two squares for a while before reading on. Square A is the same size as square B, and all the right-angled triangles inside the square are also the same size. Because the squares are equal, the white area inside them is also equal. Now, note that the big white square inside square A is the square of the hypotenuse of the riht-angled triangle. And the smaller white squares inside square B are the squares of the other two sides of the triangle. In other words, the square of the hypotenuse is equal to the square of the other two sides. Voilà.

Since we can construct a square like A and B for any shape or size of right-angled triangle, the theorem must be true in all cases.

The thrill of maths is the moment of instant revelation, from proofs such as this, when suddenly everything makes sense. It is immensely satisfying, an almost physical pleasure. The Indian mathematician Bhaskara was so taken by this proof that underneath a picture of it in his twelfth-century maths book
Lilavati
, he wrote no explanation, just the word ‘Behold!’

There are many other proofs of Pythagoras’s Theorem, and a particularly lovely one is found in the figure overleaf, credited to the Arabic mathematician Annairizi, and dated around 900
CE
. The theorem is contained within the repeating pattern. Can you spot it? (If you can’t, some help is included as an
appendix
.)

In his 1940 book
The Pythagorean Proposition
, Elisha Scott Loomis published 371 proofs of the theorem, devised by a surprisingly diverse collection of people. One dating to 1888 was attributed to E.A. Coolidge, a blind girl, another to Ann Condit, a 16-year-old high-school student, dating to 1938, while others were attributed to Leonardo da Vinci and US President James A. Garfield. Garfield had stumbled on his proof during some mathematical amusements with colleagues when he was a Republican congressman. ‘We think it something on which the members of both houses can unite without distinction of party,’ he said when the proof was first published in 1876.