Alex’s Adventures in Numberland (19 page)

The Greeks used a similar system, with alpha (
) being one, beta (ß) being two, and so on to the twenty-seventh letter of their alphabet, sampi (
), which was 900. Greek mathematical culture, the most advanced in the classical world, did not share the Indian hunger for jumbo numbers. The highest-value number word they had was
myriad
, meaning 10,000, which they wrote as a capital M.

Roman numerals were also alphabetic, although their system had more ancient roots than those of either the Greeks or the Jews. The symbol for one was I, probably a relic of a notch on a tally stick. Five was V, maybe because it looked like a hand. The other numbers were X, L, C, D and M for 10, 50, 100, 500 and 1000. All the other numbers were generated using these seven capital letters. The Roman system’s provenance from the tally stick made it a very intuitive way of writing out numbers. It was also efficient – using just seven symbols compared to 22 in Hebrew and 27 in Greek – and Roman numerals were the predominant number system in Europe for well over a thousand years.

Roman numerals, however, were very poorly suited to arithmetic. Let’s try to calculate 57×43. The best way to do this is with a method known as Egyptian or peasant multiplication, because it dates back at least to ancient Egypt. It is an ingenious method, though slow.

You first decompose one of the numbers being multiplied into powers of two (which are 1, 2, 4, 8, 16, 32 and so on, doubling each time) and make a table of the doubles of the other number. So, for the example 57×43, let us decompose 57 and draw up a table of doubles of 43. I’m using Arabic numerals to show how it’s done, and will translate into Roman numerals afterwards.

Decomposition: 57 = 32 + 16 + 8 + 1

Table of doubles:

The multiplication of 57×43 is equivalent to the addition of the numbers in the table of doubles that correspond to amounts in the decomposition. This sounds like a mouthful but is fairly straightforward. The decomposition contains a 32, a 16, an 8 and a 1. In the table, 32 corresponds to 1376, 16 corresponds to 688, 8 corresponds to 344 and 1 corresponds to 43. So, we can rewrite the initial multiplication as 1376 + 688 + 344 + 43, which equals 2451.

Now for the Roman numerals: 57 is LVII and 43 is XLIII. The decomposition and the table becomes:

and

so,

Oof! By breaking down the calculation into digestible morsels involving only doubling and adding, Roman numerals are just about up to the task. Still, we did much more work than we needed to. I mentioned earlier that the Roman system was intuitive and efficient. I’m taking that back. The Roman system quickly becomes counter-intuitive since the length of the number is not dependent on value. MMCDLI is larger than DCLXXXVIII, but uses fewer numerals, which goes against common sense. And any efficiency gained by using only seven symbols is forfeited by the inefficiency of how they are used. Often long strings are required to signify small numbers: LXXXVI uses six symbols, compared to the Arabic equivalent, 86, which uses two.

Compare the calculation above with the method of ‘long’ multiplication we all learned at school:

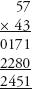
There is a very simple reason why our method is easier and quicker. Neither the Romans nor the Greeks or Jews had a symbol for zero. When it comes to sums, nothing makes all the difference.

The Vedas are Hinduism’s sacred texts. They have been passed down orally for generations until being transcribed into Sanskrit about 2000 years ago. In one of the Vedas a passage about the construction of altars lists the following number words:

With names for every multiple of ten, large numbers can be described very efficiently, which provided astronomers and astrologers (and, presumably, altar builders) with a suitable vocabulary for referring to the enormous quantities required in their calculations. This is one reason why Indian astronomy was ahead of its time. Consider the number 422,396. The Indians started at the smallest digit, at the right, and enumerated the others successively from right to left:
Six and nine dasa and three sahasra and two ayuta and two niyuta and four prayuta
. It is not too much of a step to realize that you can leave out the names for the powers of ten, since the position of the number in the list defines its value. In other words, the number above could be written:
six, nine, three, two, two, four
.

This type of enumeration is known as a ‘place-value’ system, which we discussed earlier. An abacus bead has a value dependent on which column it is in. Likewise, each number in the above list has a value dependent on its position in the list. Place-value systems, however, require the concept of a ‘place-holder’. For example, if a number has two
dasa
, no
sata
and three
sahasra
it cannot be written
two
,
three
since that refers to two
dasa
and three
sata
. A place-holder is needed to maintain the correct positions, to make it clear that there are no
sata
, and the Indians u a e word
shunya
– meaning ‘void’ – to refer to this place-holder. The number that is just two
dasa
and three
sahasra
would be written as
two, shunya, three
.

The Indians were not the first to introduce a place-holder. That honour probably went to the Babylonians, who wrote their number symbols in columns with a base 60 system. One column was for units, the next column was for 60s, the next for 3600s and so on. If a number had no value for that column, it was initially left blank. This, however, led to confusion, so they eventually introduced a symbol that denoted the absence of a value. This symbol, however, was used only as a marker.

After adopting
shunya
as a place-holder, the Indians took the idea and ran with it, upgrading
shunya
into a fully fledged number of its own: zero. Nowadays, we have no difficulty in understanding that zero is a number. But the idea was far from obvious. The Western civilizations, for example, failed to come up with it even after thousands of years of mathematical enquiry. Indeed, the scale of the conceptual leap achieved by India is illustrated by the fact that the classical world was staring zero in the face and still saw right through it. The abacus contained the concept of zero because it relied on place value. For example, when a Roman wanted to express 101, he would push a bead in the first column to signify 100, move no beads in the second column, indicating no tens, and push a bead in the third column to signify a single unit. The second, untouched column was expressing nothing. In calculations, the abacist knew he had to respect untouched columns just as he had to respect ones in which the beads were moved. But he never gave the value expressed by the untouched column a numerical name or symbol.

Zero took its first tentative steps as a bonafide number under the tutelage of Indian mathematicians such as Brahmagupta, who in the seventh century showed how
shunya
behaved towards its number siblings:

If ‘fortune’ is understood as a positive number,
a
, and ‘debt’ as a negative number, –
a
, Brahmagupta has written out the statements:

Numbers had emerged as tools for counting, as abstractions that described amounts. But zero was not a counting number in the same way; understanding its value required a further level of abstraction. Yet the less that maths was tied to actual things, the more powerful it became.

Treating zero as a number meant that the place-value system that had made the abacus the best way to calculate could be properly exploited using written symbols. Zero would enhance mathematics in other ways too, by leading to the ‘invention’ of negative numbers and decimal fractions – concepts we learn effortlessly at school and are intrinsic to our needs in daily life, but which were in no way self-evident. The Greeks made fantastic mathematical discoveries without a zero, negative numbers or decimal fractions. This was because they had an essentially spatial understanding of mathematics. To them it was nonsensical that nothing could be ‘something’. Pythagoras was no more able to imagine a negative number than a negative triangle.