Alex’s Adventures in Numberland (21 page)

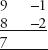
The second part of the answer is calculated by multiplying the two numbers in the second column (–1×–2 = 2). The complete answer is 72.

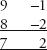
I find this trick immensely satisfying. Writing out a single-digit number next to its difference from ten is somehow like pulling it apart to reveal its inner personality, lining up the ego and alter ego. We get a deeper understanding of how the number behaves. A sum such as 9×8 is about as mundane as they come, yet scratch the surface and we see unexpected elegance and order. And the method works not just for 9×8 but for any two numbers. Tirthaji chalked up another example: 8×7.

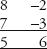
Again, the first digit can be derived in any one of the four ways: 8 + 7 – 10 = 5, or –2 – 3 + 10 = 5, or 8 – 3 = 5 or 7 – 2 = 5. The second digit is the product of the digits in the second column, –2
^×
–3 = 6.

Tirthaji’s tactic reduces the multiplication of two single-digit numbers to an addition and the multiplication of the differences of the original numbers from ten. In other words, it reduces the multiplication of two single digit numbers larger than five to an addition and the multiplication of two numbers less than five. Which means that it is possible to multiply by six, seven, eight and nine without going higher than our five-times table. This is useful to people who find learning their times tables difficult.

In fact, the technique explained by Tirthaji is the same as a method of finger calculation used at least since the Renaissance in Europe, and still used by farmhands in parts of France and Russia as late as the 1950s. On each hand the fingers are assigned the numbers from 6 to 10. To multiply two numbers together, say 8 and 7, touch the 8 finger to Weinger. The number of digits above the linking fingers on one side is subtracted from the linking finger on the other side (either 7 – 2 or 8 – 3) to give 5. The number of digits above the linking fingers on each side, 2 and 3, are multiplied to make 6. The answer, as above, is 56.

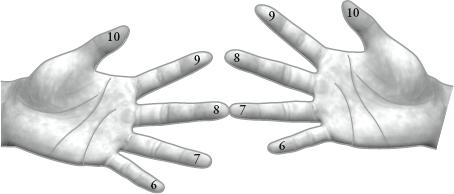
How to calculate 8
×
7 with ‘peasant’ finger multiplication.

Tirthaji continued his talk by demonstrating that the method also works when multiplying two-digit numbers, this time using the example 77×97. He wrote on the board:

Then, instead of writing the difference of 77 from 10, he wrote the difference of each number from 100. (This is where the second sutra comes in. When subtracting a number from 100, or any larger power of 10, all the digits of the number are subtracted from 9 apart from the last one, which is subtracted from 10, as I showed on chapter 3):

As before, in order to get the first part of the answer there are four options. He chose to show the two diagonal additions: 77 – 3 = 97 – 23 = 74.

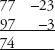
The second part is derived by multiplying both digits in the right-hand column: –23×–3 = 69.

The answer is 7469.

Tirthaji then proceeded to an example with three figures: 888×997. This time the difference is calculated from 1000.

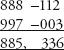
Diagonal addition gives 885 for the first part, and multiplication of the right column gives 336 for the second, for an answer of 885,336.

‘Equations are rendered much easier by these formulae,’ Tirthaji commented. The students reacted with spontaneous hearty laughter. Perhaps the chuckles came from the absurdity of an 82-year-old guru in a robe teaching basic arithmetic to some of the smartest maths students in the US. Or perhaps it was in appreciation of the playfulness of Tirthaji’s arithmetical tricks. Arabic numerals are a mine of hidden patterns, even at such a simple level as multiplying two single digits together. Tirthaji then tinued his talk with techniques for squaring, dividing and algebra. The response seems to have been enthusiastic, judging by a transcription made of the lecture notes: ‘Immediately following the end of the demonstration, one student was heard to ask his friend beside him, “What do you think?” His friend’s reply, “Fantastic!”’

On his return to India, Tirthaji was summoned to the holy city of Varanasi, where a special council of Hindu elders discussed his breach of protocol in leaving the country. It was decided that his trip was to be the first and last time that a Shankaracharya was allowed to travel abroad, and Tirthaji undertook a purification ritual just in case he had consumed unHindu food while on his travels. Two years later, he passed away.

In my hotel in Puri I met up with two leading proponents of Vedic Mathematics to learn more about it. Kenneth Williams is a 62-year-old former maths teacher from southern Scotland who has written several books about the method. ‘It is so beautifully presented and so unified as a system,’ he told me. ‘When I first found out about it I thought this is the way mathematics ought to be.’ Williams was a subdued, gentle man with a priestly forehead, trim salt-and-pepper beard and heavy-lidded blue eyes. With him was the much more talkative Gaurav Tekriwal, a 29-year-old stockbroker from Kolkata, who was wearing a crisp white shirt and Armani shades. Tekriwal is president of the Vedic Maths Forum India, an organization that runs a website, arranges talks and sells DVDs.

Tekriwal had helped me secure an audience with the Shankaracharya, and he and Williams wanted to accompany me. We hailed a motor rickshaw and set off to the Govardhan Math, an auspicious name but one that, unfortunately, has nothing to do with maths. It means monastery, or temple. We passed the seafront and small streets lined with stalls selling food and patterned silk. The Math is a plain brick and concrete building the size of a small country church, surrounded by palm trees and a sand garden planted with basil, aloe vera and mango. In the courtyard is a banyan tree, its trunk decorated with ochre cloth, where Shankara, the eighth-century Hindu sage who founded the order, is believed to have sat and meditated. The only modern touch was a shiny black frontage on the first floor – a bullet-proof façade that was installed to protect the Shankaracharya’s room after the Math received Muslim terrorist threats.

The current Shankaracharya of Puri, Nischalananda Sarasvati, inherited the position from the man who inherited it from Tirthaji. He is proud of Tirthaji’s mathematical legacy, and has published five books on the Vedic approach to numbers and calculation. On reaching the Math we were ushered into the room the Shankaracharya uses for his audiences. The only pieces of furniture were an antique sofa with deep red upholstery and, immediately in front of it, a low chair with a large seat and wooden back covered in a red shawl: the Shankaracharya’s throne. We sat facing it, cross-legged on the floor, and waited for the holy man to arrive.

Sarasvati entered the room, wearing a faded pink robe. His senior disciple stood up to recite some religious verses, and then Sarasvati clasped his hands in prayer, touching the image of Shankara on the back wall. He had blue eyes, a white beard and a light-skinned, bald pate. Sitting down in a half lotus on his throne, he assumed an expression between serene and glum. As the session was about to begin, a man in blue robes dived in front of me, throwing himself prostrate before the throne with outstretched hands. Sighing like an exasperated grandfather, taracharya nonchalantly shooed him away.