Alex’s Adventures in Numberland (20 page)
Read Alex’s Adventures in Numberland Online
Authors: Alex Bellos

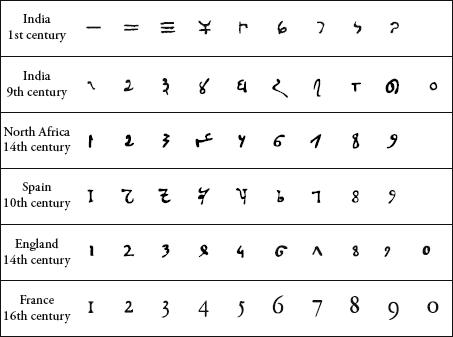
Evolution of modern numerals.
Of all the innovative ways that numbers were treated in ancient India, perhaps none was more curious than the vocabulary used to describe the numbers from zero to nine. Rather than each digit having a unique name, there was a colourful lexicon of synonyms. Zero, for example, was
shunya
, but it was also ‘ether’, ‘dot’, ‘hole’ or the ‘serpent of eternity’. One could be ‘earth’, ‘moon’, ‘the pole star’ or ‘curdled milk’. Two was interchangeable with ‘arms’, three with ‘fire’ and four with ‘vulva’. The names that were chosen depended on context and conformed to Sanskrit’s strict rules of versification and prosody. For example, the following verse is a piece of number-crunching from an ancient astrological text:
The apsides of the moon in a yuga
Fire. Vacuum. Horsemen.
Vasu
*
. Serpent. Ocean, and of its waning nodeVasu
. Fire. Primordial Couple. Horsemen. Fire. Twins.
The translation is:
[The number of revolutions] of the apsides of the moon in a [cosmic cycle is]
Three. Zero. Two. Eight. Eight. Four, [or 488,203] and of its waning node
Eight. Three. Two. Two. Three. Two. [or 232,238]
While at first it might seem confusing to have flowery alternatives for each digit, it actually makes perfect sense. During a period in history when manuscripts were flimsy and easily spoiled, astronomers and astrologers needed a backup method to remember significant numbers accurately. Strings of digits were more easily memorized when described in verse with varied names, rather than when using the same number names repeatedly.
Another reason why numbers were passed down orally was that the numerals that were emerging in different regions of India for the numbers from one to nine (zero, I will come to later) were not the same. Two people who did not understand each other’s number symbols could at least communicate numbers using words. By 500
CE
, however, there was greater uniformity in the numerals used, and India had the three elements that were required for a modern decimal number system: ten numerals, place value, and an all-singing, all-dancing zero.
Owing to its ease of use, the Indian method spread to the Middle East, where it was embraced by the Islamic world, which accounts for why the numerals have come to be known, erroneously, as Arabic. From there they were brought to Europe by an enterprising Italian, Leonardo Fibonacci, his last name meaning ‘son of Bonacci’. Fibonacci was first exposed to the Indian numerals while growing up in what is now the Algerian city of Béjaïa, where his father was a Pisan customs official. Realizing that they were much better than Roman ones, Fibonacci wrote a book about the decimal place-value system called the
Liber Abaci
, published in 1202. It opens with the happy news:
The nine Indian figures are:
9 8 7 6 5 4 3 2 1
With these nine figures, and with the sign 0, which the Arabs call
zephyr
, any number whatsoever is written, as will be demonstrated.
More than any other book, the
Liber Abaci
introduced the Indian system to the West. In it Fibonacci demonstrated ways to do arithmetic that were quicker, easier and more elegant than the methods the Europeans had been using. Long multiplication and long division might seem dreary to us now, but at the beginning of the thirteenth century they were the latest technological novelty.
Not everyone, however, was convinced to switch immediately. Professional abacus operators felt threatened by the easier counting method, for one thing. (They would have been the first to realize that the decimal system was essentially the abacus with written symbols.) On top of that, Fibonacci’s book appeared during the period of the Crusades against Islam, and the clergy was suspicious of anything with Arab connotations. Some, in fact, considered the new arithmetic the Devil’s work precisely because it was so ingenious. A fear of Arabic numerals is revealed through the etymology of some modern words. From
zephyr
came ‘zero’ but also the Portuguese word
chifre
, which means ‘[Devil] horns’, and the English word
cipher
, meaning ‘code’. It has been argued that this was because using numbers with a
zephyr
, or zero, was done in hiding, against the wishes of the Church.

Arithmetica, the spirit of arithmetic, adjudicates between Boethius, who is using Arabic numerals, and Pythagoras, who has a counting board. Her adoring gaze and the numbers on her dress give away which method she prefers. From a woodblock engraving in Greorius Reisch’s
Margarita Philosophica
(1503).
In 1299 Florence banned Arabic numerals because, it was said, the slinky symbols were easier to falsify than solid Roman Vs and Is. A 0 could easily become a 6 or 9, and a 1 morph seamlessly into a 7. As a consequence, it was only around the end of the fifteenth century that Roman numerals were finally superseded, though negative numbers took much longer to catch on in Europe, gaining acceptance only in the seventeenth century, because they were said to be used in calculations of illegal money-lending, or usury, which was associated with blasphemy. In places where no calculation is needed, however, such as legal documents, chapters in books and dates at the end of BBC programmes, Roman numerals still live on.
With the adoption of Arabic numbers, arithmetic joined geometry to become part of mathematics in earnest, having previously been more of a tool used by shopkeepers, and the new system helped open the door to the scientific revolution.
A more recent Indian contribution to the world of numbers is a set of arithmetical tricks collectively known as Vedic Mathematics. It was discovered at the beginning of the twentieth century by a young swami, Bharati Krishna Tirthaji, who claimed to have found them in the Vedas, which was rather like, say, a vicar announcing he had found a method for solving quadratic equations in the Bible. Vedic Mathematics is based on the following list of 16 aphorisms, or sutras, which Tirthaji said were not actually written in any passage of the Vedas, instead being detectable only ‘on the basis of intuitive revelation’.
- By one more than the one before
- All from 9 and the last from 10
- Vertically and Cross-wise
- Transpose and Apply
- If the Samuccaya is the Same it is Zero
- If One is in Ratio the Other is Zero
- By Addition and by Subtraction
- By the Completion or Non-Completion
- Differential Calculus
- By the Deficiency
- Specific and General
- The Remainders by the Last Digit
- The Ultimate and Twice the Penultimate
- By One Less than the One Before
- The Product of the Sum
- All the Multipliers
Was he serious? Yes, and very much so too. Tirthaji was one of the most respected holy men of his generation. A former child prodigy, graduating in Sanskrit, philosophy, English, maths, history and science at the age of 20, he was also a talented orator who, it became clear early into adulthood, was destined to take a prominent role in Indian religious life. In 1925 Tirthaji was indeed made a Shankaracharya, one of the senior positions in traditional Hindu society, in charge of a nationally important monastery in Puri, Orissa, on the Bay of Bengal. This is the town thatI was visiting, the focus of the Rath Yatra chariot festival, where I was hoping to meet the incumbent Shankaracharya, who is the current ambassador for Vedic Mathematics.
In his role as Shankaracharya in the 1930s and 1940s, Tirthaji regularly toured India, giving sermons to crowds of tens of thousands, usually dispensing spiritual guidance but also promoting his new way of calculation. The 16 sutras, he taught, were to be used as if they were mathematical formulae. While they might have sounded ambiguous, like chapter titles in an engineering book or numerological mantras, they in fact referred to specific rules. One of the most straightforward is the second,
All from 9 and the last from 10
. This is to be implemented whenever you are subtracting a number from a power of ten, such as 1000. If I want to calculate 1000 – 456, for example, then I subtract 4 from 9, 5 from 9 and 6 from 10. In other words, the first two numbers from 9 and the last from 10. The answer is 544. (The other sutras are applications for other situations, more of which I will introduce later.)
Tirthaji promoted Vedic Mathematics as a gift to the nation, arguing that maths that usually took schoolchildren 15 years to learn could, with the sutras, be learned in just eight months. He even went as far as claiming that the system could be expanded to cover not just arithmetic but algebra, geometry, calculus and astronomy. Due to Tirtharji’s moral authority and charisma as a public speaker, audiences loved him. The general public, he wrote, were ‘highly impressed, nay, thrilled, wonder-struck and flabbergasted!’ at Vedic Mathematics. To those who asked whether the method was maths or magic, he had a set reply: ‘It is both. It is magic until you understand it; and it is mathematics thereafter.’
In 1958, when he was 82 years old, Tirthaji visited the United States, which caused much controversy back home because Hindu spiritual leaders are forbidden from travelling abroad, and it was the first time that a Shankaracharya had ever left India. His trip provoked great curiosity in the US. The West Coast would later become a focus for flower power, gurus and meditation, but back then no one had seen anyone like him. When Tirthaji arrived in California the
Los Angeles Times
called him ‘one of the most important – and least-known – personages in the world’.
Tirthaji had a full schedule of talks and TV appearances. Though he spoke mostly about world peace, he devoted one lecture entirely to Vedic Mathematics. The venue was the California Institute of Technology, one of the most prestigious scientific institutions in the world. Tirthaji, who weighed not much more than seven stone and was wearing traditional robes, sat in a chair at the front of a wood-panelled classroom. In a quiet voice, but with a commanding presence, he told his audience: ‘I have been, from my childhood, equally fond of metaphysics on the one side and mathematics on the other. And I’ve found no difficulty at all.’
He went on to explain exactly how he had found the sutras, asserting that there was a wealth of hidden knowledge in the Vedic texts that came from the many double meanings of words and phrases. These mystical ‘puns’, he added, had been totally lost on Western Indologists. ‘The supposition is that mathematics was not part of the Vedic literature,’ he said, ‘but when I was able to find it, well, it was easy sailing.’
Tirthaji’s opening trick was to demonstrate how to multiply 9×8 without using a multiplication table. This uses the sutra
, although why it does so only becomes clear later.
First, he drew a 9 on the blackboard, followed by the difference of 9 from 10, which is –1. Underneath he drew 8 and next to it the difference of 8 from 10, which is –2.
9 | –1 |
8 | –2 |
The first number of the answer can be derived in four different ways. Either add the numbers in the first column and subtract ten (9 + 8 – 10 = 7). Or add the numbers in the second column and add ten (–1 – 2 + 10 = 7) or add either of the diagonals (9 – 2 = 7, and 8 – 1 = 7). The answer is always seven.