Alex’s Adventures in Numberland (22 page)
Read Alex’s Adventures in Numberland Online
Authors: Alex Bellos
Religious procedure requires the Shankaracharya to speak Hindi, so I used his senior disciple as an interpreter. My first question was ‘How is maths linked to spirituality?’ After several minutes the reply came back. ‘In my opinion, the creation, the standing and the destruction of this whole universe happens in a very mathematical form. We do not differentiate between mathematics and spirituality. We see mathematics as the fountainhead of Indian philosophies.’
Sarasvati then told a story about two kings who met in a forest. The first king told the other that he could count all the leaves on a tree just by looking at it. The second king doubted him and started tearing off the leaves to count them one by one. When he had finished he arrived at the precise number given by the first king. Sarasvati said the story was evidence that the ancient Indians had the ability to count large numbers of objects by looking at them as a whole instead of enumerating them individually. This and many other skills from that era, he added, had been lost. ‘All these lost sciences can be regained by the help of serious contemplation, serious meditation and serious effort,’ he said. The process of studying the ancient scriptures with the intention of rescuing ancient knowledge, he added, is exactly what Tirthaji had done with mathematics.
During the interview the room filled up with about 20 people, who sat silently as the Shankaracharya spoke. As the session drew to a close, a middle-aged software consultant from Bangalore asked a question about the significance of the number 10
62
. The number was in the Vedas, he said, so it had to mean something. The Shankaracharya agreed. It was in the Vedas and, yes, it had to mean something. This prompted a discussion about how the Indian government is neglecting the country’s heritage, and the Shankaracharya lamented that he spent most of his energy in trying to protect traditional culture so he could not devote more time to maths. This year he had managed only 15 days.
Over breakfast the next day I asked the computer consultant about his interest in the number 10
62
, and he answered with a lecture on the scientific achievements of ancient India. Thousands of years ago, he said, Indians understood more about the world than what is known today. He mentioned that they flew aeroplanes. When I asked if there was any proof of this, he replied that stone engravings of millennia-old aircraft have been found. Did these planes use the jet engine? No, he said, they were powered using the Earth’s magnetic field. They were made from a composite material and flew at a low speed, between 100 and 150kmph. He then became increasingly annoyed by my questions, interpreting my desire for proper scientific explanations as an affront to Indian heritage. Eventually, he refused to speak to me.
While Vedic science is fantastical, occultist and barely credible, Vedic Mathematics stands up to scrutiny, even though the sutras are mostly so vague as to be meaningless and to accept the story of their origin in the Vedas requires the suspension of disbelief. Some of the techniques are so specific as to be nothing more than curiosities – such as a tip for calculating the fraction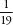
in decimal. But some are very neat indeed.
Consider the example of 57
×
43 from earlier. The standard method of multiplying these numbers is to write down two intermediary lines, and then add them:
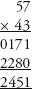
Using the third sutra,
Vertically and Cross-wise
, we can find the answer quite handily as follows.
Step 1:
Write the numbers on top of each other:
|
|
|
|
Step 2:
Multiply the digits in the right-hand column: 7×3 = 21. The final digit of this number is the final digit of the answer. Write it below the right-hand column, and carry the 2.
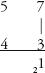
Step 3:
Find the sum of the cross-wise products: (5 × 3) + (7 × 4) = 15 + 28 = 43. Add the 2 that is carried from the previous step to get 45. The final digit of this number, the 5, is written underneath the left-hand column, with 4 carried.
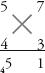
Step 4:
Multiply the digits in the left-hand column, 5×4 = 20. Add the 4 that has been carried to make 24, to give the final answer:
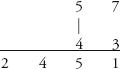
The numbers have been multiplied vertically and cross-wise, as the sutra said on the tin. This method can be generalized to multiplications of numbers of any size. All that changes is that more numbers need to be vertically and cross-multiplied. For example, 376×852:
|
|
|
|
|
|
Step 1:
We start with the right column: 6×2 = 12
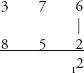
Step 2:
Then the sum of the cross-products between the units and the tens column, (7 × 2) + (6 × 5) = 44, plus the 1 carried above. This is 45.
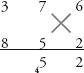
Step 3:
Now we move to the cross-products between the units and the hundreds column, and add them to the vertical product of the tens column, (3 × 2) + (8 × 6) + (7 × 5) = 89, plus the 4 carried above. This is 93.
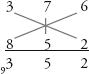
Step 4:
Moving leftwards, we now cross-multiply the first two columns: (3 × 5) + (7 × 8) = 71, plus the 9 carried above. This is 80.
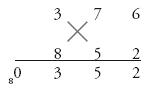
Step 5:
Finally, we find the vertical product of the left column, 3 × 8 = 24, plus 8 carried above. This is 32. The final answer: 320,352.
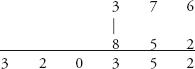
Vertically and Cross-wise
, or ‘cross-multiplication’, is faster, uses less space and is less laborious than long multiplication. Kenneth Williams told me that whenever he explains the Vedic method to school pupils they find it easy to understand. ‘They can’t believe they weren’t taught it before,’ he said. Schools favour long multiplication because it spells out every stage of the calculation.
Vertically and Cross-wise
keeps some of the machinery hidden. Williams thinks this is no bad thing, and may even help less bright pupils. ‘We have to steer a path and not insist that kids have to know everything all of the time. Some kids need to know how [multiplication] works. Some don’t want to know how it works. They just want to be able to do it.’ If a child ends up not being able to multiply because the teacher insists on teaching a general rule that he or she cannot grasp, he said, then the child is not being educated. For the smarter kids, added Williams, Vedic Maths brings arithmetic alive. ‘Mathematics is a creative subject. Once you have a variety of methods, children realize you can invent your own and they become inventive too. Maths is a really fun, playful subject and [Vedic Maths] brings out a way to teach it that way.’
My first audience with the Shankaracharya had not covered all intended topics of discussion, so I was granted a second one. At the beginning of the session, the senior disciple had an announcement to make: ‘We would like to say something about zero,’ he said. The Shankaracharya then spoke for about ten minutes in Hindi in an animated manner, with the disciple then translating: ‘The present mathematical system considers zero as a non-existent entity,’ he declared. ‘We want to rectify this anomaly. Zero cannot be considered a non-existent entity. The same entity cannot be existing in one place and non-existing somewhere else.’ The thrust of the Shankaracharya’s argument was, I think, the following: people consider the 0 in 10 to exist, but 0 on its own not to exist. This is a contradiction – either something exists or it does not. So zero exists. ‘In Vedic literature zero is considered as the everlasting number,’ he said. ‘Zero cannot be annihilated or destroyed. It is the indestructible base. It is the basis of everything.’