Alex’s Adventures in Numberland (26 page)
Read Alex’s Adventures in Numberland Online
Authors: Alex Bellos

Dase used this series:
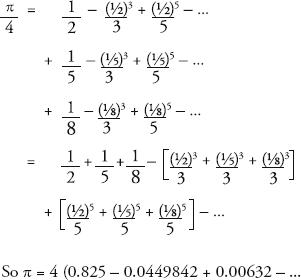
After one term this is
3.3After two terms this is
3.1200After three terms this is
3.1452
Dase barely had time to rest on his laurels before the Brits decided to covet his achievement, and within a decade William Rutherford had calculated pi to 440 places. He encouraged his protégé William Shanks, an amateur mathematician who ran a boarding school in County Durham, to go even further. In 1853 he reached 607 digits, and by 1874 he was at 707. His record held for 70 years until D.F. Ferguson, of the Royal Naval College in Chester, found a mistake in Shanks’s calculation. He had made an error at the 527th place so all the subsequent numbers were wrong. Ferguson spent the last year of the Second World War calculating pi longhand. One can only assume that he thought the war was already won. By May 1945 he had 530 places, and by July 1946 he reached 620, and no one has ever calculated further using only paper and pen.
Ferguson was the last of the manual digit-hunters and the first of the mechanical. Using a desk calculator he added almost another 200 places in just over a year, so in September 1947 pi was known to 808 decimal places. Computers then changed the race. The first of them to battle pi was the Electronic Numerical Integrator and Computer, or ENIAC, which was built in the final years of the Second World War at the US Army’s Ballistic Research Laboratory in Maryland. It was the size of a small house. In September 1949 the ENIAC took 70 hours to calculate pi to 2037 digits – smashing the record by more than a thousand decimal places.
As more and more digits were found in pi, one thing seemed pretty clear: the numbers obeyed no obvious pattern. Yet it was only in 1767 that mathematicians were able to prove that the higgledy-piggledy sequence of digits would never repeat itself. The discovery followed from considering what type of number pi might be.
The most familiar
type
of number is the
natural numbers
. They are the counting numbers starting at one:
1, 2, 3, 4, 5, 6…
The natural numbers, however, are limited in scope because they expand in only one direction. More ul are the
integers
, which are the natural numbers together with zero and the negatives of the natural numbers:
… –4, –3, –2, –1, 0, 1, 2, 3, 4…
The integers cover every positive or negative whole number from minus infinity to plus infinity. If there were a hotel with an unlimited amount of floors and an unlimited amount of lower and lower basements, the buttons in the elevator would be the integers.
Another basic type of number is the
fraction
, which are the numbers written when
a
and
b
are integers but
b
is not 0. The top number in a fraction is the
numerator
and the bottom number is the
denominator
. If we have several fractions, the
lowest common denominator
is the lowest number that can be divided by all the denominators without leaving a remainder. So, if we have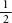 and
and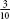 , the lowest common denominator is 10, since both 2 and 10 divide into 10. What about the lowest common denominator of
, the lowest common denominator is 10, since both 2 and 10 divide into 10. What about the lowest common denominator of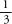 ,
,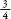 ,
,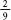 and
and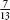 ? In other words, what is the smallest number that 3, 4, 9 and 13 divide into? The answer is surprisingly big: 468! I mention this to make a semantic rather than a mathematical point. The phrase ‘lowest common denominator’ is often used to describe something basic or unsophisticated. It sounds evocative, but misrepresents the arithmetic. Lowest common denominators can often be big and unconventional: 468 is quite an impressive number! A more arithmetically meaningful phrase for something mainstream and cheap is
? In other words, what is the smallest number that 3, 4, 9 and 13 divide into? The answer is surprisingly big: 468! I mention this to make a semantic rather than a mathematical point. The phrase ‘lowest common denominator’ is often used to describe something basic or unsophisticated. It sounds evocative, but misrepresents the arithmetic. Lowest common denominators can often be big and unconventional: 468 is quite an impressive number! A more arithmetically meaningful phrase for something mainstream and cheap is
highest common factor
– which is the largest number that can be divided into every one of a group of numbers. The highest common factor of 3, 4, 9 and 13, for example, is 1, and you can’t get much lower or more unsophisticated than that.
Since fractions are equivalent to ratios between integers, they are also called
rational numbers
, and there is an infinite amount of them. In fact, there is an infinite number of rational numbers between 0 and 1. For example, let’s take every fraction where the numerator is 1 and the denominator is a natural number bigger than or equal to 2. This is the set composed of:
We can go further and prove that there is an infinite number of rational numbers between
any two
rational numbers. Let
c
and
d
be any two rational numbers, with
c
less than
d
. The point halfway between
c
and
d
is a rational number: it is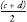 . Call this point
. Call this point
e
. We can now find a point halfway between
c
and
e
. It is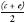 . It is rational and also between
. It is rational and also between
c
and
d
. We can carry on ad infinitum, always splitting the distance between
c
and
d
into smaller and smaller parts. No matter how tiny the distance between
c
and
d
is in the first place, there will always n infinite amount of rational numbers in between them.