Alex’s Adventures in Numberland (27 page)

Since we can always find an infinite number of rational numbers between any two rational numbers, it might be thought that the rational numbers cover every number. Certainly, this is what Pythagoras had hoped. His metaphysics was based on the belief that the world was made up of numbers and the harmonic proportions between them. The existence of a number that could not be described as a ratio diminished his position, at the very least, if it did not contradict it outright. Yet unfortunately for Pythagoras, there
are
numbers that cannot be expressed in terms of fractions, and – rather embarrassingly for him – it is his own theorem that leads us to one. If you have a square where each side has length 1, then the length of the diagonal is the square root of two, which cannot be written as a fraction. (I have included a proof as an
appendix
.)

Numbers that cannot be written as fractions are called
irrational
. According to legend, their existence was first proved by the Pythagorean disciple Hippasus, which did not endear him to the Brotherhood; he was declared a heretic and was drowned at sea.

When a rational number is written out as a decimal fraction, either it has a finite amount of digits, in the way that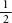
can be written 0.5, or the expansion will end up repeating itself, just as
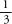is 0.3333…where the 3s go on for ever. Sometimes the recurring loop is more than one digit, as is the case of
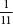, which is 0.090909…where the digits 09 repeat for ever, or
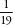, which is 0.0526315789473684210…where 052631578947368421 repeats for ever. By contrast, and this is the crucial point, when a number is irrational its decimal expansion never repeats.

In 1767 the Swiss mathematician Johann Heinrich Lambert proved that pi was indeed irrational. The early pi-men may have hoped after the initial chaos of 3.14159…that the noise would calm and a pattern ensue. Lambert’s discovery confirmed that this was impossible. Pi’s decimal expansion cavorts towards infinity in a predestined yet apparently indiscriminate way.

Mathematicians interested in the irrationals wanted to categorize them further. In the eighteenth century they started to speculate about a special type of irrational called
transcendental numbers
. These were numbers so mysterious and evasive that finite mathematics could not capture them. The square root of two,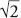
, for example, is irrational but can be described as the solution to the equation
x
²
= 2. A transcendental number is an irrational that cannot be described by an equation with a finite amount of terms. When the concept of transcendental numbers was first mooted, no one knew if they even existed.

They did exist, although it took about a hundred years before Joseph Liouville, a French mathematician, came up with a few examples. Pi was not among them. Only after another 40 years did the German Ferdinand von Lindemann prove that pi was indeed transcendental. The number existed beyond the realm of finite algebra.

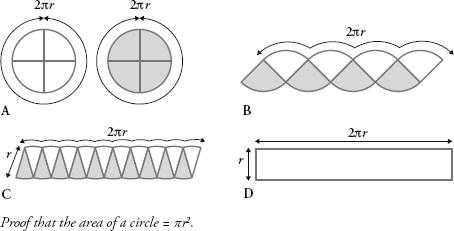
Lindemann’s discovery was a milestone for number theory. It also settled, once and for all, what was probably the most celebrated unsolved problem in mathematics: whether or not it was ple to square the circle. In order to explain how it did this, however, I need to introduce the formula that says that the area of a circle is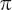
r
²
, where
r
is the radius. (The radius is the distance from the centre to the side, or half the diameter.) A visual proof of why this is true is an instance where a pie is the best metaphor for pi. Imagine you have two same-sized circular pies, a white one and a grey one, as below in A. The circumference of each pie is pi times the diameter, or pi times twice the radius, or 2p
r
. When sliced into equal segments the pieces can be rearranged, as in B with quarter segments, or as in C with ten segments. In both cases the length of the side remains 2p
r
. If we keep on slicing smaller and smaller segments, then the shape would eventually become a rectangle, as in D, with sides
r
and 2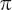
r
. The area of the rectangle – which is the area of the two pies – is therefore 2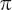
r
²
, so the area of one pie is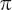
r
²
.