Alex’s Adventures in Numberland (23 page)

By now I was used to the Shankaracharya’s distinctive mix of mathematics and metaphysics. I had given up asking him to clarify certain points since by the time my comments had been translated into Hindi, discussed and then translated back, the answers inevitably added to my confusion. I decided to stop concentrating on the details of his speech, and let the translated words just float over me. I looked at the Shankaracharya closely. He was wearing an orange robe today, tied with a big knot behind his neck, and his forehead had been daubed with beige paint. I wondered what it would be like to live the way he did. I had been told that he sleeps in an unfurnished room, eats the same bland curry every day, and that he has no need or desire for possessions. Indeed, at the beginning of the session a pilgrim had approached him to give him a bowl of fruit, and as soon as he received it, he had given the fruit away to the rest of us. I got a mango, which was by my feet.

Trying to experience the Shankaracharya’s wisdom in a different way, I thought of the phrase ‘zero is an existent entity’ and repeated it like a mantra in my head. I let go. Suddenly I am lost in my thoughts. And it all makes sense. ‘Zero is an existent entity’ is not just the Shankaracharya’s mathematical point of view, but a pithy phrase of self-description. Sitting in front of me is Mr Zero himself, the embodiment of
shunya
in flesh and bone.

It was a moment of clarity, maybe even of enlightenment. Nothing was not nothing in Hindu thought. Nothing was everything. And the monastic, self-abnegating Shankaracharya was a perfect ambassador for this nothingness. I thought about the deep connection between Eastern spirituality and mathematics. Indian philosophy had embraced the concept of nothingness just as Indian maths had embraced the concept of zero. The conceptual leap that led to the invention of zero happened in a culture that accepted the void as the essence of the universe.

The symbol that emerged in ancient India for zero perfectly encapsulated the Shankaracharya’s overriding message that mathematics cannot be separated from spirituality. The circle, 0, was chosen because it portrays the cyclical movements of the face of heaven. Zero means nothing, and it means eternity.

Pride in the invention of zero has helped make mathematical excellence an aspect of Indian national identity. Schoolchildren must learn their times tables up to 20, which is twice as high as I was taught growing up in the UK. In previous decades Indians were required to learn their tables up to 30. One of India’s top non-Vedic mathematicians, S.G. Dani, attested to this: ‘As a child I did have this impression of mathematics being extremely important,’ he told me. It was always common for elder people to set children mathematical challenges, and it was greatly appreciated if they got the answers right. ‘Irrespective of whether it is useful or not, maths is something that is valued in India by one’s peer group and friends.’

Dani is senior professor of mathematics at the Tata Institute of Fundamental Research in Bombay. He has an academic’s comb-over frizz, rimmed tortoiseshell glasses and a moustache that frames the length of his upper lip. And he is no fan of Vedic Mics; he neither believes that Tirthaji’s arithmetical methods can be found in the Vedas nor does he believe it is particularly helpful to say that they do. ‘There are many better ways to bringing interest into mathematics than resorting to inputting them into ancient texts,’ he said. ‘I don’t believe that they are making mathematics interesting. The selling point is that these algorithms make you fast, not that it makes it interesting, not that it makes you internalize what is going on. The interest is in the end, not the process.’ He is doubtful they do make calculation quicker, since real life does not throw up such perfectly formed problems as finding the decimal breakdown of 1/19. At the end of the day, he added, the conventional method is more convenient.

So, I was surprised that Dani spoke empathetically of Tirthaji’s mission with Vedic Maths. Dani related to Tirthaji on an emotional level. ‘The dominant feeling that I had for him is that he had this inferiority complex that he was trying to conquer. As a child I also had this kind of attitude. In India in those days [shortly after Independence] there was a strong feeling that we needed to get back [from the British] what we lost by hook or by crook. It was mostly in terms of artefacts, stuff that the British might have taken away. Because we lost such a lot, I thought we should have the equivalent back of what we lost.

‘Vedic Mathematics is a misguided attempt to claim arithmetic back for India.’

Some of the tricks of Vedic Mathematics are so simple that I wondered if I might come across them anywhere else in arithmetical literature. I thought that Fibonacci’s
Liber Abaci
would be a good place to start. When I got back to London I found a copy at the library, opened the chapter on multiplication and Fibonacci’s first suggested method is none other than…
Vertically and Cross-wise
. I did some more research and discovered that multiplication using
All from 9 and the last from 10
was a favoured technique in several books from sixteenth-century Europe. (In fact, it has been suggested that both methods might have influenced the adoption of×as the multiplication sign. When×made its first appearance as a notation for multiplication in 1631, books had already been published illustrating the two multiplication methods with large ×s drawn as cross-lines.)

Tirthaji’s Vedic Mathematics is, it would seem, at least in part, a rediscovery of some very common Renaissance arithmetical tricks. They may or may not have come from India originally, but whatever their provenance, the charm of Vedic Mathematics for me is the way it encourages a childlike joy in numbers and the patterns and symmetries they hold. Arithmetic is essential in daily life and important to do properly, which is why we are taught it so methodically at school. Yet in our focus on practicalities we have lost sight of quite how amazing the Indian number system is. It was a dramatic advance on all previous counting methods and has not been improved upon in a thousand years. We take the decimal place-value system for granted, without realizing how versatile, elegant and efficient it is.

In the early nineteenth century, news of boy wonder George Parker Bidder, the son of a Devonshire stonemason, reached the ears of Queen Charlotte. She had a question for him:

‘From the Land’s-end, Cornwall, to Farret’s-head, in Scotland, is found by measurement to be 838 miles; how long would a snail be creeping that distance, at the rate of 8 feet per day?’

The exchange and the answer – 553,080 days – is mentioned in a popular book of the time,
A short Account of George Bidder, the celebrated Mental Calculator: with a Variety of the most difficult Questions, Proposed to him at the principal Towns in the Kingdom, and his surprising rapid Answers!
The pages list the child’s greatest calculations, including such classics as ‘What is the square root of 119,550,669,121?’ (345,761, answered in half a minute) and ‘How many pounds weight of sugar are there in 232 hogsheads, each weighing 12cwt. 1qr. 22lbs?’ (323,408lbs, also answered in half a minute.)

Arabic numerals made doing sums easier for everyone, but an unexpected consequence was the discovery that certain people were blessed with truly astonishing arithmetical skills. Often, these prodigies excelled in no other way than their facility with numbers. One of the earliest-known examples was a Derbyshire farmhand, Jedediah Buxton, who amazed locals with his abilities in multiplication despite being barely able to read. He could, for example, calculate the value of a farthing when doubled 140 times. (The answer is 39 digits long, with 2 shillings 8 pence left over.) In 1754, curiosity about Buxton’s talent led to him being invited to visit London, where he was examined by members of the Royal Society. He seems to have had some of the symptoms of high-functioning autism, for when he was taken to see Shakespeare’s
Richard III
he was left nonplussed by the experience, although he notified his hosts that the actors had taken 5202 steps and spoken 14,445 words.

In the nineteenth century ‘lightning calculators’ were international stage stars. Some showed aptitude at an extraordinarily young age. Zerah Colburn, from Vermont, was five when he gave his first public demonstration and eight when he sailed to England with dreams of big-time success. (Colburn was born with hexadactyly, but it is not known if his extra fingers gave him an advantage when learning to count.) A contemporary of Colburn’s was the Devonshire lad George Parker Bidder. The two prodigies crossed paths in 1818, when Colburn was 14 and Bidder 12, and the encounter, in a London pub, inevitably led to a maths duel.

Colburn was asked how long it would take a balloon to circumnavigate the globe if the balloon were travelling at 3878 feet per minute and the world were 24,912 miles around. It was a suitably international question for the unofficial title of smartest alec on Earth. But after deliberating for nine minutes, Colburn failed to give an answer. A London newspaper gushed that his opponent, on the other hand, took only two minutes before giving the correct reply, ‘23 days, 13 hours and 18 minutes, [which] was received with marks of great applause. Many other questions were proposed to the American boy, all of which he refused answering; while young Bidder replied to all.’ In his charming autobiography,
A memoir of Zerah Colburn, written by himself
, the American gives a different version of the contest. ‘[Bidder] displayed great strength and power of mind in the higher branches of arithmetic,’ he said, before adding dismissively, ‘but he was unable to extract the roots, and find the factors of numbers.’ The mpionship was left undecided. Edinburgh University subsequently offered to take over Bidder’s education. He went on to become an important engineer, at first in railroads and eventually supervising construction of London’s Victoria Docks. Colburn, on the other hand, returned to America, became a preacher and died aged 35.

The ability to calculate rapidly has no great correlation with mathematical insight or creativity. Only a few great mathematicians have demonstrated lightning-calculator skills, and many mathematicians have surprisingly poor arithmetic. Alexander Craig Aitken was a well-known lightning calculator in the first half of the twentieth century, unusual in that he was also a professor of mathematics at Edinburgh University. In 1954 Aitken gave a lecture to the Society of Engineers in London, in which he explained some of the methods in his repertoire, such as algebraic shortcuts and – crucially – the importance of memory. To prove his point he rattled off the decimal expansion for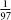
, which repeats only after 96 digits.

Aitken ended his talk with the rueful comment that when he acquired his first desk calculator his abilities began to deteriorate. ‘Mental calculators may, like the Tasmanian or the Moriori, be doomed to extinction,’ he predicted. ‘Therefore…you may be able to feel an almost anthropological interest in surveying a curious specimen, and some of my auditors here may be able to say in the year 2000 ce, “Yes, I knew one such.”’

This was one calculation, however, that Aitken got wrong.

‘Neurons! On the ready! Go!’

With an impatient snap and swoosh, the contestants in the multiplication round at the Mental Calculation World Cup turned over their papers. The room at Leipzig University was silent as the 17 men and two women contemplated the first question: 29,513,736× 92,842,033.

Arithmetic is back in vogue. Thirty years after the first cheap electronic calculators precipitated a widespread demise in mental calculation skills, a backlash is under way. Newspapers offer up daily maths brainteasers, popular computer games with arithmetic puzzles sharpen our minds and – at the high end – lightning calculators compete in regular international tournaments. The Mental Calculation World Cup was founded in 2004 by German computer scientist Ralf Laue, and takes place every two years. It was the inevitable culmination of Laue’s two hobbies: mental arithmetic and collecting unusual records (such as the Most Grapes Thrown over a Distance of 15ft and Caught in the Mouth in One Minute, which is 55 of them). The internet helped, enabling him to meet kindred spirits – mental arithmeticians are not, in general, extroverts. The global community of human calculators, or ‘mathletes’, was well represented in Leipzig, with contestants from countries as diverse as Peru, Iran, Algeria and Australia.

How do you measure calculating skills? Laue adopted the categories already chosen by
Guinness World Records
– the multiplication of two eight-digit numbers, the addition of ten ten-digit numbers, extracting the square root of six-figure numbers to eight significant figures, and finding the day of the week of any date between 1600 and 2100. The latter is known as a calendar calculation, and is a flashback to the golden age of lightning calculation, when performers would ask a member of the audience their birth date and then instantly name the day of the week it fell on.

Regulation, and a spirit of competitiveness, have come at the expense of theatrics. The youngest contestant at the World Cup, an 11-year-old boy from India, performed the ‘air abacus’ – his hands were jerking wildly around rearranging imaginary beads, while all the others were quiet and still, occasionally jotting down their answers. (The rules say that only the final answer can be written down.) After 8 minutes and 25 seconds, Alberto Coto of Spain stuck his hand up like an excited schoolboy. The 38-year-old had completed ten multiplications of two eight-digit numbers in that time, smashing the world record. It was evidently an awesome accomplishment, yet watching him was as compelling as invigilating an exam.

Conspicuously absent from proceedings in Leipzig, however, was perhaps the world’s most famous mathlete, the French student Alexis Lemaire, who prefers another yardstick to measure computational power. In 2007 Lemaire, aged 27, made international headlines when, at the Science Museum in London, he took just 70.2 seconds to calculate the thirteenth root of:

Lemaire’s achievement was undoubtedly the more spectacular. The number has 200 digits, which can barely be pronounced in 70.2 seconds. But did his feat mean that, as he claims, he is the greatest lightning calculator of all time? This is a matter of deep controversy in the calculation milieu, mirroring the battle almost 200 years ago between Zerah Colburn and George Bidder, both exceptional at their own type of sum.

The term ‘thirteenth root of
a
’ refers to the number that when multiplied by itself 13 times equals
a
. Only a fixed amount of numbers when multiplied by themselves 13 times equal a 200-digit number. (It is a large fixed amount. The answer is limited to about 400 trillion possibilities, all 16 digits long and beginning with 2.) Because 13 is prime and considered unlucky, Lemaire’s calculation was vested with an extra aura of mystery. In fact, 13 brings with it some advantages. For instance when 2 is multiplied by itself 13 times, the answer ends in 2. When 3 is multiplied by itself 13 times the answer ends in 3. The same is true for 4, 5, 6, 7, 8 and 9. In other words, the last digit of the thirteenth root of a number is the same as the last digit of the original number. We get this number for free, without having to do any calculation.

Lemaire has worked out algorithms, which he has not divulged, to calculate the other 14 digits in the final answer. Purists, possibly unfairly, say that his skill is less a feat of calculation and more one of memorizing huge strings of numbers. And they point out that Lemaire cannot find the thirteenth root of
any
200-digit number given to him. At the Science Museum in London he was presented with several hundred numbers and allowed to select the one that he would do the calculation for.

Still, Lemaire’s performance was more in keeping with the tradition of the stage calculators of old. Audiences want to feel the ‘wow’, rather than understand the process. By contrast, at the Mental Calculation World Cup, Coto had no choice about the problem to be solved and used no hidden techniques when he multiplied 29,513,736×92,842,033. He simply used his 1-to 9-times tables. The fastest way to multiply eight digits by eight digits is using the Vedic sutra
Vertically and Cross-Wise
, which breaks the sum into 64 multiplications of single-digit figures. He managed to get the right answer in an average of less than 51 seconds. Knowing what he was doing made it less dazzling, even though it was obviously still a formidable feat.

As I talked with competitors in Leipzig, I discovered that many of them had fallen in love with speed arithmetic thanks to Wim Klein, a Dutch lightning calculator who was a celebrity in the 1970s. Klein was already a veteran of circuses and music halls when, in 1958, he was given a job by Europe’s top physics institute – the European Organization for Nuclear Research (CERN) in Geneva, providing calculations for the physicists. He was probably the last human calculator to have been employed as one. As computers developed, his skills became redundant, and in retirement he returned to showbiz, appearing frequently on TV. (Klein, in fact, was one of the first to promote thirteenth-root calculations.)

A century before Klein another human calculator, Johann Zacharias Dase, was also employed by the scientific establishment to do their sums for them. Dase was born in Hamburg and started performing as a lightning calculator in his teens, when he was taken under the wing of two eminent mathematicians. In the days before electronic or mechanical calculators, scientists relied on logarithm tables to do complicated multiplications and divisions. As I will explain in more detail later, every number has its own logarithm, which can be calculated using a laborious procedure of adding fractions. Dase calculated the natural logarithms of the first 1,005,000 numbers, each to seven decimal places. It took him three years, and he said he enjoyed the task. Then, on the recommendation of the mathematician Carl Friedrich Gauss, Dase embarked on another enormous project: compiling a table of factors of all the numbers between 7,000,000 and 10,000,000. This means he looked at every number in the range and calculated its factors, which are the whole numbers that divide that number. For example, 7,877,433 has only two factors: 3 and 2,625,811. When Dase died, aged 37, he had completed a substantial part of it.

Yet it was another calculation for which Dase is best remembered. When still a teenager he calculated pi to 200 places, a record for the time.

Circles are everywhere in the natural world – you see them in the full moon, in the eyes of humans and animals and in the cross-section of an egg. Tie a dog to a post and the path it patrols when the lead is taut is a circle. The circle is the simplest two-dimensional geometrical shape. An Egyptian farmer counting how much of a crop to plant in a round field, or a Roman mechanic measuring the length of wood for a wheel would have needed to make calculations involving circles.