Alex’s Adventures in Numberland (54 page)

The golden angle.

The golden angle explains why you generally find on a plant stem that the number of leaves and number of turns before a leaf sprouts more or less directly above the first one is a Fibonacci number. For example, roses have 5 leaves every 2 turns, asters have 8 leaves for every 3 turns and almond trees have 13 leaves every 5 turns. Fibonacci numbers occur because they provide the nearest whole-number ratios for the golden angle. If a plant sprouts 8 leaves for every 3 turns, each leaf occurs every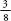
turn, or every 135 degrees, a very good approximation for the golden angle.

The unique properties of the golden angle are most strikingly seen in seed arrangements. Imagine that a flower head produces seeds from the centre point at a fixed angle of rotation. When new seeds emerge, they push the older seeds further out from the centre. These three diagrams show the patterns of seeds that emerge with three different fixed angles: just below the golden angle, the golden angle, and just above.

What is surprising is how a tiny change in the angle can cause such a huge variation in the positions of the seeds. At the golden angle, the seed head is a mesmerizing pattern of interlocking logarithmic spirals. It is the most compact arrangement possible. Nature chooses the golden angle because of this compactness – the seeds are bound together more closely and the organism will be stronger because of it.

In the late nineteenth century the German Adolf Zeising most forcefully put forth the view that the golden proportion is beauty incarnate, describing the ratio as a universal law ‘which permeates, as a paramount spiritual ideal, all structures, forms and proportions, whether cosmic or individual, organic or inorganic, acoustic or optical; which finds its fullest realization, however, in the human form’. Zeising was the first person to claim that the front of the Parthenon is in the shape of a golden rectangle. In fact, there is no documentary evidence that those in charge of the architectural project, who included the sculptor Phidias, used the golden ratio. Nor, if you look closely, is the golden rectangle a precise fit. The edges of the pedestal fall outside. Yet it was Phidias’s connection to the Parthenon that, in around 1909, inspired the American mathematician Mark Barr to name the golden ratio phi.

Despite the eccentric tone of Zeising’s work, he was taken seriously by Gustav Fechner, one of the founders of experimental psychology. In order to discover if there was any empirical evidence that humans thought the golden rectangle more beautiful than any other sort of rectangle, Fechner devised a test in which subjects were shown a number of different rectangles and asked which they preferred.

Fechner’s results appeared to vindicate Zeising. The rectangle closest to a golden one was the top choice, favoured by just over a third of the sample group.ven though Fechner’s methods were crude, his rectangle-testing began a new scientific field – the experimental psychology of art – as well as the narrower discipline of ‘rectangle aesthetics’. Many psychologists have conducted similar surveys on the attractiveness of rectangles, which is not as absurd as it sounds. If there were a ‘sexiest’ rectangle, this shape would be of use to the designers of commercial products. Indeed, credit cards, cigarette packets and books often approach the proportions of a golden rectangle. Unfortunately for phi-philes, the most recent and detailed piece of research, by a team led by Chris McManus of University College London, suggests that Fechner was wrong. The 2008 paper stated that ‘more than a century of experimental work has suggested that the golden section actually plays little normative role in subjects’ preferences for rectangles’. Yet the authors did not conclude that analysing rectangle preference is a waste of time. Far from it. They claimed that while no one rectangle is universally preferred by humans, there are important individual differences in the aesthetic appreciation of rectangles that merit further investigation.

Lesser scientists than Fechner were also inspired by Zeising’s theories. Frank A. Lonc from New York measured the height of 65 women compared to the height of their belly buttons and discovered that the ratio was 1.618. He had excuses when it wasn’t: ‘Subjects whose measurements did not fall within this ratio testified to hip injuries or other deforming accidents in childhood.’ The French architect Le Corbusier created ‘Modulor man’ in order to use proper proportions in architecture and design. In his man, the ratio of the height of the man to the height of his belly button is 1829/1130, or 1.619, and the ratio of the distance between his belly button and his upheld right hand and his belly button and his head is 1130/698, again 1.619. Le Corbusier’s intention for the Modulor was to use these proportions in architecture and design.

Gary Meisner is a 53-year-old business consultant from Tennessee. He calls himself the Phi Guy and on his website sells merchandise including phi T-shirts and mugs. His bestselling product, however, is the PhiMatrix, a piece of software that creates a grid on your computer screen to check images for the golden ratio. Most purchasers use it as a design tool to make cutlery, furniture and homes. Some customers use it for financial speculation by superimposing the grid on graphs of indices and using phi to predict future trends. ‘A guy in the Caribbean was using my matrix to trade in oil, a guy in China was using it to trade in currencies,’ he said. Meisner was drawn to the golden mean because he is spiritual and says it helped him understand the universe, but even the Phi Guy thinks that his fellow travellers can go too far. He is, for example, unconvinced by the traders. ‘When you look back on the market it is pretty easy to find relationships that conform to phi,’ he said. ‘The challenge is that looking backwards is completely different to looking out the front window.’ Meisner’s website has made him the go-to guy for every flavour of phi aficionado. He told me that a month ago he received an email from an unemployed man who believed that the only way to get a job interview was to design his résumé in the proportions of the golden ratio. Meisner felt the man was deluded and took pity on him. He gave him some phi design tips, but suggested that it would be more fruitful investing in more traditional job-hunting methods such as business networking. ‘I got a letter from him this morning,’ Meisner blurted. ‘He said he has a job interview. He is giving credit to the résuménew design!’

Back in London I told Eddy Levin the story of the golden résumé as an example of excessive eccentricity. Levin, however, didn’t think it was funny. In fact, he agreed that a phi-proportioned résumé was better than a regular one. ‘It would look more beautiful, and so the reader would be more attracted to it.’

After 30 years of studying the golden ratio, Levin is convinced that wherever there is beauty, there will be phi. ‘Any art which looks good, the dominant proportions are the golden proportion,’ he said. He knows this is an unpopular viewpoint, as it prescribes a formula for beauty, but he guarantees he will be able to find phi in any piece of art.

My instinctive reaction to Levin’s phi obsession was one of scepticism. For a start, I was unconvinced that his gauge was accurate enough to measure 1.618 sufficiently precisely. It was not surprising to find a ratio of ‘approximately phi’ in a painting or a building, especially if you could select which parts to choose. Also, since the ratio of consecutive Fibonacci numbers makes a good approximation to 1.618, whenever there is a grid of 5×3 or 8×5 or 13×8 and so on, you will see a golden rectangle. Of course the ratio will be a common one.

Yet there was something compelling about Levin’s examples. I felt the thrill of wonder with each new image he showed me. Phi really was everywhere. Yes, the golden ratio has always attracted cranks, but this in itself did not mean that all the theories were crankish. Some very respectable academics have claimed that phi creates beauty, particularly in the structure of musical compositions. The argument that human beings might be drawn to a proportion that best expresses natural growth and regeneration does not seem too far-fetched.

It was a sunny summer’s day and Levin and I relocated to his garden. We sat on two lawn chairs and sipped tea. Levin told me that the limerick was a successful form of poetry because the syllables in its lines (8, 8, 5, 5, 8) are Fibonacci numbers. Then I had an idea. I asked Levin if he knew what an iPod was. He didn’t. I had one in my pocket and I took it out. It was a beautiful object, I said, and according to his reasoning, it should contain the golden ratio.

Levin took my shiny white iPod and held it in his palm. Yes, he replied, it was beautiful, and it should. Not wanting to get my hopes up, he warned me that factory-produced objects often do not follow the golden ratio perfectly. ‘The shape shifts slightly for the convenience of manufacture,’ he said.

Levin opened his callipers and started measuring between all the significant points.

‘Ooh, yes,’ he grinned.

It used to be said that you go to Las Vegas to get married and to Reno to get a divorce. Now you can visit both cities for their slot machines. With 100 slot machines, Reno’s Peppermill Casino isn’t even the largest casino in town. Walking through its main hall, the roulette and blackjack tables were shadowy and subdued in comparison to the flashing, spinning, beeping regiments of slots. Technological evolution has deprived most one-armed bandits of their lever limbs and mechanical insides. Players now bet by pressing lit buttons or touch-screen displays. Occasionally I heard the rousing sound of clattering change, but this came from pre-recorded samples since coins have been replaced by electronic credits.

Slots are the casino industry’s cutting edge; its front line and its bottom line. The machines make $25 billion a year in the United States (
after
they’ve paid out all their prize money), which is about two and a half times the total value of movie tickets sold in the country annually. In Nevada, the global centre of casino culture, slots now make up almost 70 percent of gambling revenue – and the number nudges higher every year.

Probability is the study of chance. When we flip a coin, or play the slots, we do not know how the coin will land, or where the spinning reels will stop. Probability gives us a language to describe how likely it is that the coin will come up heads, or that we will hit the jackpot. With a mathematical approach, unpredictability becomes very predictable. While we take this idea for granted in our daily lives – it is implicit, for example, whenever we read the weather forecast – the realization that maths can tell us about the future was a very profound and comparatively recent idea in the history of human thought.

I had come to Reno to meet the mathematician who sets the odds for more than half of the world’s slot machines. His job has historical pedigree – probability theory was first conceived in the sixteenth century by the gambler Girolamo Cardano, our Italian friend we met earlier when discussing cubic equations. Rarely, however, has a mathematical breakthrough arisen from such self-loathing. ‘So surely as I was inordinately addicted to the chess board and the dicing table, I know that I must rather be considered deserving of the severest censure,’ he wrote. His habit yielded a short treatise called
The Book on Games of Chance
, the first scientific analysis of probability. It was so ahead of its time, however, that it was not published until a century after his death.

Cardano’s insight was that if a random event has several equally likely outcomes, the chance of any individual outcome occurring is equal to the proportion of that outcome to all possible outcomes. This means that if there is a one-in-six chance of something happening, then the chance of it happening is one sixth. So, when you roll a die, the chance of getting a six is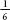
. The chance of throwing an even number is
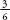. The chance of throwing an even number is
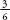. which is the same as
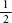. Probability can be defined as the likelihood of something happening expressed as a fraction. Impossibility has a probability of 0; certainty, a probability of 1; and the rest is in between.

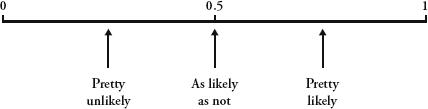
This seems straightforward, but it isn’t. The Greeks, the Romans and the ancient Indians were all obsessive gamblers. None of them, though, attempted to understand how randomness is governed by mathematical laws. In Rome, for exale, coins were flipped as a way of settling disputes. If the side with the head of Julius Caesar came up, it meant that he agreed with the decision. Randomness was not seen as random, but as an expression of divine will. Throughout history, humans have been remarkably imaginative in finding ways to interpret random events. Rhapsodomancy, for example, was the practice of seeking guidance through chance selection of a passage in a literary work. Similarly, according to the Bible, picking the short straw was an impartial way of selecting only in so far as God let it be that way: ‘The lot is cast into the lap; but the whole disposing thereof is of the Lord’ (Proverbs 16: 33).

Superstition presented a powerful block against a scientific approach to probability, but after millennia of dice-throwing, mysticism was overcome by perhaps a stronger human urge – the desire for financial profit. Girolamo Cardano was the first man to take Fortune hostage. It could be argued, in fact, that the invention of probability was the root cause of the decline, over the last few centuries, of superstition and religion. If unpredictable events obey mathematical laws, there is no need to have them explained by deities. The secularization of the world is usually associated with thinkers such as Charles Darwin and Friedrich Nietzsche, yet quite possibly the man who set the ball rolling was Girolamo Cardano.

Games of chance have most commonly involved dice. A model popular in antiquity was the
astragalus
– an anklebone from a sheep or a goat – that had four distinctly flat faces. Indians liked dice in the shape of rods and Toblerones, and they marked the different faces with pips, the most likely explanation for which is that dice predate any formal system of numerical notation, and this tradition has survived. The fairest dice have identical sides, and if one imposes the further condition that each side must also be a regular polygon, there are only five shapes that fit the bill, the Platonic solids. All the Platonic solids have been used as dice. Ur, possibly the world’s oldest known game, which dates from at least as far back as the third century bc, used a tetrahedron, which, however, is the worst of the five choices because the tetrahedron hardly rolls and has only four sides. Octahedrons (eight sides) were used in ancient Egypt, and dodecahedrons (twelve) and icosahedrons (twenty) are still found in fortune-tellers’ handbags.

By far the most popular dice shape has been the cube. It is the easiest to make, its span of digits is neither too big nor too small, it rolls nicely but not too easily, and it’s obvious on which number it lands. Cubical dice with pips are a cross-cultural symbol of luck and chance, as comfortable bashed around in Chinese mah-jong salons as they are dangling from the rear-view mirrors of British cars.

As I mentioned earlier, roll one die and the chance of a six is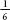
. Roll another die and the chance of a six is also
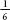. What is the chance of rolling a pair of dice and getting a pair of sixes? The most basic rule of probability is that the chances of two independent events happening is the same thing as the chance of one event happening
multiplied
by the chance of the second event happening. When you throw a pair of dice the outcome of the first die is independent of the outcome of the second, and vice versa. So, the chances of throwing two sixes is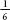
×
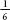, or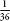
. You can see this visuallgits iounting all the possible combinations of two dice: there are 36 equally likely outcomes and only one of them is a six and a six.