Alex’s Adventures in Numberland (55 page)

Conversely, of the 36 possible outcomes, 35 of them are
not
double six. So, the probability of not throwing a six and a six is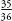
. Rather than counting up 35 examples, you can equally start with the full set and then subtract the instances of double sixes. In this example, 1 –
=
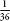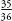. The probability of something not happening, therefore, is 1 minus the probability of that thing happening.

The dicing table was an early equivalent of the slot machine, where gamblers placed wagers on the outcome of dice throws. One classic gamble was to roll four dice and bet on the chance of at least one six appearing. This was a nice little earner for anyone willing to put money on it, and we already have enough maths knowledge to see why:

A probability of 0.518 means that if you threw four dice a thousand times, you could expect to get at least one six about 518 times, and get no sixes about 482 times. If you gambled on the chance of at least one six, you would win on average more than you would lose, so you would end up profiting.

The seventeenth-century writer Chevalier de Méré was a regular at the dicing table, as he was at the most fashionable salons in Paris. The chevalier was as interested in the mathematics of dicing as he was in winning money. He had a couple of questions about gambling, though, that he was unable to answer himself, so in 1654 he approached the distinguished mathematician Blaise Pascal. His chance enquiry was the random event that set in motion the proper study of randomness.

Blaise Pascal was only 31 when he received de Méré’s queries, but he had been known in intellectual circles for almost two decades. Pascal had shown such gifts as a young child that at 13 his father had let him attend the scientific salon organized by Marin Mersenne, the friar and prime-number enthusiast, which brought together many famous mathematicians, including René Descartes and Pierre de Fermat. While still a teenager, Pascal proved important theorems in geometry and invented an early mechanical calculation machine, which was called the Pascaline.

The first question de Méré asked of Pascal concerned double sixes. As we saw above, there is a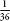
chance of getting double six when you throw two dice. The overall chance of getting a double six increases the more times you throw the pair of dice. The chevalier wanted to know how many times he needed to throw the dice to make gambling on the occurrence of a double six a good bet.

His second question was more complex. Say Jean and Jacques are playing a dice game consisting of several rounds in which both roll a die to see who gets the highest number. The outright winner is whoever rolls the highest number three times. Each has a stake of 32 francs, so the pot is 64 francs. If the game has to be terminated after three rounds, when Jean has rolled the highest number twice and Jacques once, how should the pot be divided up?

Pondering the answers, and feeling the need to discuss them with a fellow genius, Pascal wrote to his old friend from the Mersenne salon, Pierre de Fermat. Fermat lived far from Paris, in Toulouse, an appropriately named city for someone analysing a problem about gambling. He was 22 years older than Pascal and worked as a judge at the local criminal court, dabbling in maths only as an intellectual recreation. Nevertheless, his amateur ruminations had made him one of the most respected mathematicians of the first half of the seventeenth century.

The short correspondence between Pascal and Fermat about chance – which they called
hasard
– was a landmark in the history of science. Between them the men solved both of the literary bon vivant’s problems, and in so doing, set the foundations of modern probability theory.

Now for the answers to Chevalier de Méré’s questions. How many times do you need to throw a pair of dice so that it is more likely than not that a double six will appear? In one throw of two dice the chance of a double six is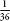
, or 0.028. The chance of a double six appearing in two throws of two dice is 1 minus the probability of no double sixes appearing in two throws, or 1 – (
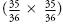). This works out to be
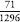, or 0.055. (Note: the chance of a double six in two throws is
not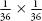
. This is the chance of a double six in both throws. The probability we are concerned with is the chance of
at least one
double six, which includes the outcomes of either a double six in the first throw, in the second throw, or in both throws. The gambler needs only one double six to win, not a double six in both.) The chances of a double six in three throws of two dice are 1 minus the probability of no doubles, which this time is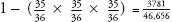
0.081. As we can see, the more times one throws the dice, the higher the probability of throwing a double six: 0.028 with one throw, 0.055 with two, and 0.081 with three. Therefore, the original question can be rephrased as ‘After how many throws does this fraction exceed 0.5?’, as a probability of more than a half means that the event is more likely than not. Pascal calculated correctly that the answer is 25 throws. If the chevalier gambled on the chance of a double six in 24 throws, he could expect to lose money, but after 25 throws, the odds shift in his favour and he could expect to win.