Alex’s Adventures in Numberland (58 page)

Baerlocher and I met at IGT’s head office in a Reno business park, a 20-minute drive from the Peppermill Casino. He walked me through the production line, where tens of thousands of slot machines are built every year, and past a storage hall where hundreds were neatly stacked in rows. Baerlocher was clean-shaven and preppy, with short dark hair and a dimple in his chin. Originally from Carson City, half an hour’s drive away, he joined IGT after completing a maths degree at Notre Dame University, Indiana. For someone who loved inventing games as a child, and discovered a talent for probability at college, the job was a perfect fit.

When I wrote earlier that the core concept of gambling was the notion of expected value, I was giving only half the story. The other half is what mathematicians call the
law of large numbers
. If you bet only a few times on roulette or on the slots, you might come out on top. The more you play roulette, however, the more likely it is that you will lose overall. Payback percentages are only true in the long run.

The law of large numbers says that if a coin is flipped three times, it might not come up heads at all, but flip it three billion times and you can be pretty sure that it wil come up heads almost exactly 50 percent of the time. During the Second World War, the mathematician John Kerrich was visiting Denmark when he was arrested and interned by the Germans. With time on his hands, he decided to test the law of large numbers and flipped a coin 10,000 times in his prison cell. The result: 5067 heads, or 50.67 percent of the total. Around 1900, the statistician Karl Pearson did the same thing 24,000 times. With significantly more trials, you would expect the percentage to be closer to 50 percent – and it was. He threw 12,012 heads, or 50.05 percent.

The results mentioned above seem to confirm what we take for granted – that in a coin flip the outcome of heads is equally likely as the outcome of tails. Recently, however, a team at Stanford University led by the statistician Persi Diaconis investigated whether heads really are as likely to show up as tails. The team built a coin-tossing machine and took slow-motion photography of coins as they spun through the air. After pages of analysis, including estimates that a nickel will land on its edge in about 1 in 6000 throws, Diaconis’s results appeared to show the fascinating and surprising result that a coin will, in fact, land on the same face from which it was launched about 51 percent of the time. So, if a coin is launched heads up, it will land on heads slightly more often than it will land on tails. Diaconis concluded, though, that what his research really proved was how difficult it is to study random phenomena and that ‘for tossed coins, the classical assumptions of independence with probability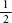
are pretty solid’.

Casinos are all about large numbers. As Baerlocher explained, ‘Instead of just having one machine [casinos] want to have thousands because they know if they get the volume, even though one machine maybe what we call “upside-down” or losing, the group as a collective has a very strong probability of being positive for them.’ IGT’s slots are designed so that the payback percentage is met, within an error of 0.5 percent, after ten million games. At the Peppermill, where I was staying during my visit to Reno, each machine racks up about 2000 games a day. With almost 2000 machines, this makes a daily casino rate of four million games a day. After two and a half days, the Peppermill can be almost certain that it will be hitting its payback percentage within half a percent. If the average bet is a dollar, and the percentage is set to 95 percent, this works out to be $500,000 in profit, give or take $50,000, every 60 hours. It is little wonder, then, that slots are increasingly favoured by casinos.

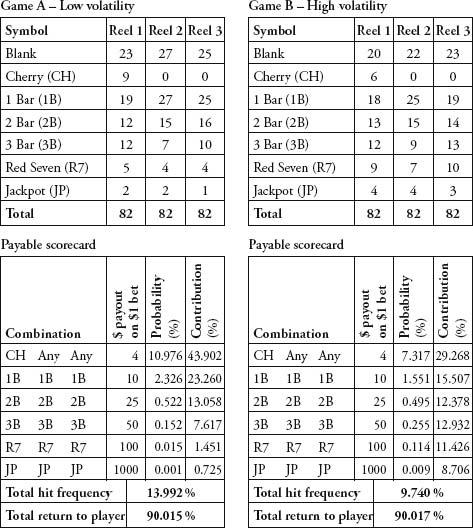
The rules of roulette and craps haven’t changed since the games were invented centuries ago. By contrast, part of the fun of Baerlocher’s job is that he gets to devise new sets of probabilities for each new slot machine that IGT introduces to the market. First, he decides what symbols to use on the reel. Traditionally, they are cherries and bars, but they are now as likely to be cartoon characters, Renaissance painters, or animals. Then he works out how often these symbols are on the reel, what combinations result in payouts, and how much the machine pays out per winning combination.

Baerlocher drew me up a simple game, Game A opposite, which has three reels and 82 positions per reel made up of cherries, bars, red sevens, a jackpot and blanks. If you read the table, you can see that there is a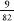
or 10.976 percent chance of cherry coming up on the first reel, and when this happens $1 wins a $4 payout. The probability of a winning combination multiplied by the payout is called the
expected contribution
. The expected contribution of cherry-aning-anything is 4×10.967 = 43.902 percent. In other words, for every $1 put into the machine, 43.902 cents will be paid out on cherry-anything-anything. When he is designing games, Baerlocher needs to make sure the sum of expected contributions for all payouts equals the desired payback percentage of the whole machine.

The flexibility of slot design is that you can vary the symbols, the winning combinations and the payouts to make very different games. Game A is a ‘cherry dribbler’ – a machine that pays out frequently, but in small amounts. Almost half of the total payout money is accounted for in payouts of just $4. By contrast, in Game B only a third of the payout money goes on $4 payouts, leaving much more money to be won in the larger jackpots. Game A is what is called a low-volatility game, while Game B is high-volatility – you hit a winning combination less often, but the chances of a big win are greater. The higher the volatility, the more short-term risk there is for the slot operator.

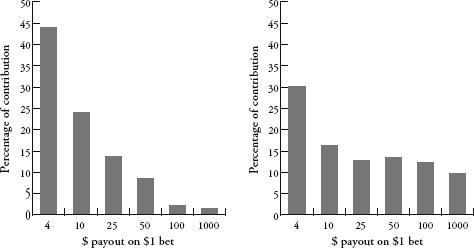
Some gamblers prefer low-volatility slots, while others prefer high. The game designer’s chief role is to make sure the machine pays out just enough for the gambler to want to continue playing – because the more someone plays, on average, the more he or she will lose. High volatility generates more excitement – especially in a casino, where machines hitting jackpots draw attention by erupting in spine-tingling
son et lumière
. Designing a good game, however, is not just about sophisticated graphics, colourful sounds and entertaining video narratives – it’s also about getting the underlying probabilities just right. I asked Baerlocher whether by playing around with volatility it was possible to design a low-payback machine that was more attractive to gamblers than a higher-payback machine. ‘My colleague and I spent over a year mapping things out and writing down some formulas and we came up with a method of hiding what the true payback percentage is,’ he said. ‘We’re now hearing from some casinos that they are running lower-payback machines and that the players can’t really pick up on it. It was a big challenge.’

I asked if this wasn’t a touch unethical.

‘It’s something that’s necessary,’ he replied. ‘We want the players to still enjoy it but we need to make sure that our customers make money.’

Baerlocher’s pay tables are helpful not just in order to understand the inner constitutions of one-armed bandits; they are also illustrative in explaining how the insurance industry works. Insurance is very much like playing the slots. Both are systems built on probability theory in which the losses of almost everyone pay for the winnings of a few. And both can be fantastically profitable for those controlling the payback percentages.

An insurance premium is no different from a gamble. You are betting on the chance that, for example, your house will be burgled. If your house is burgled, you receive a payout, which is the reimbursement for what was stolen. If your house isn’t burgled you, of course, receive nothing. The actuary at the insurance company behaves exactly like Anthony Baerlocher at IGT. He knows how much he wants to pay back to customers overall. He knows the probability for each payout event (a burglary, a fire, serious illness, etc.), so he works out how much his payouts should be per event so that the sum of expected contributions equals the total payback amount. Although compiling insurance tables is vastly more complicated than creating slot machines, the principle is the same. Since insurance companies pay out less than they receive in premiums, their payout percentage is less than 100 percent. Buying an insurance policy is a negative-expectation bet and, as such, it is a bad gamble.

So why do people take out insurance if it’s such a bad deal? The difference between insurance and gambling in casinos is that in casinos you are (hopefully) gambling with money you can afford to lose. With insurance, however, you are gambling to protect something you cannot afford to lose. While you will inevitably lose small amounts of money (the premium), this guards you against losing a catastrophic amount of money (the value of the contents of your house, for example). Insurance offers a good price for peace of mind.

It follows, however, that insuring against losing a non-catastrophic amount of money is pointless. One example is insuring against loss of a mobile phone. Mobile phones are relatively cheap (say, £100), but phone insurance is expensive (say, £7 per month). On average you will be better off if you don’t take out insurance, and instead buy yourself a new phone on the occasions that you lose it. In this way, you are ‘self-insuring’ and keeping the insurance company’s profit margins for yourself.

One reason for recent growth in the slots market is the introduction of ‘progressive’ machines, which have little to do with enlightened social policy and lots to do with the dream of instant wealth. Progressive slots have higher jackpots than other machines because they are joined in a network, with each machine contributing a percentage to a communal jackpot, the value of which gets progressively larger. In the Peppermill I had been struck by rows of linked machines offering prizes in the tens of thousands of dollars.

Progressive machines have high volatility, which means that in the short term casinos can lose significant sums. ‘If we put out a game with a progressive jackpot, about one in every twenty [casino owners] will write us a letter telling us our game is broken. Because this thing hit two or three jackpots in the first week and the machines are $10,000 in the hole,’ Baerlocher said, finding it ironic that people who are trying to profit from probability still have trouble understanding it on a basic level. ‘We’ll do an analysis and see the probability of it happening is, say, 200 to 1. They had [results] that should only happen half of a percent of the time – it had to happen to someone. We tell them, ride it out, it’s normal.’