Alex’s Adventures in Numberland (53 page)

Levin scoured photographs and discovered that in the most attractive sets of teeth, the big top front tooth (the central incisor) was wider than the one next to it (the lateral incisor) by a factor of phi. The lateral incisor was also wider than the adjacent tooth (the canine) by a factor of phi. And the canine was wider than one next to it (the first premolar) by a factor of phi. Levin wasn’t measuring the size of actual teeth, but the size of teeth in pictures when taken head-on. Still, he felt like he had made an historic discovery: the beauty of a perfect smile was prescribed by phi.

‘I was very excited,’ remembered Levin. At work, he mentioned his findings to colleagues, but they dismissed him as an oddball. He continued to develop his ideas nonetheless, and in 1978 he published an article expounding them in the
Journal of Prosthetic Dentistry
. ‘From then, people got interested in it,’ he said. ‘Now there is not a lecture that is given on [dental] aesthetics that doesn’t include a section on the golden proportion.’ Levin was using phi so much in his work that in the early 1980s he asked an engineer to design him an instrument that could tell him if two teeth were in the golden proportion. The result was the three-pronged Golden Mean Gauge. He still sells them to dentists around the world.

I couldn’t tell if Levin’s own teeth were in the golden proportion, although there was certainly a fair amount of gold in them. Levin told me his gauge became more than a work tool, and he started to measure objects other than teeth. He found phi in the patterns of flowers, in the spread of branches along stems, and in leaves along branches. He took it with him on holiday and found phi in the proportions of buildings. He also found phi in the rest of the human body, in the length of knuckles to fingers and in the relative positions of the nose, teeth and chin. Additionally, he noticed that most people use phi in their handwriting, just as hown in mine.

The more Levin looked for phi, the more he found it. ‘I found so many coincidences, I started to wonder what it was all about.’ He opened his laptop and showed me a slideshow of images, each with the three points of the gauge showing exactly where the ratio was to be found. I saw pictures of butterfly wings, peacock feathers and animal colourings, the ECG reading of a healthy human heart, paintings by Mondrian and a car.

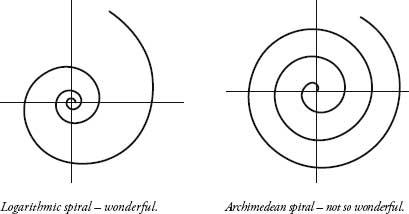
When a rectangle is constructed so that the ratio between its sides is phi, you get what is known as a ‘golden rectangle’. This rectangle has the convenient property that if we were to cut it vertically so that one side is a square, then the other side is also a golden rectangle. The mother gives birth to a baby daughter.

Golden rectangle and logarithmic spiral.

We can continue this process to create granddaughters, great-granddaughters, ad infinitum. Now, let’s draw a quarter-circle in the largest square by using a compass, placing the point at the bottom right corner and moving the pencil from one adjacent corner to the other. Repeat in the second-largest square with the compass point at the bottom left corner, with the pencil continuing the curve for another quarter-circle, and then carry on with the smaller squares. The curve is an approximation of a
logarithmic spiral
.

A true logarithmic spiral will pass through the same corners of the same squares, yet it will wind itself smoothly, unlike the curve in the diagram, which will have small jumps in curvature where the quarter-circle sections meet. In a logarithmic spiral, a straight line from the centre of the spiral – the ‘pole’ – will cut the spiral curve at the same angle at all points, which is why Descartes called the logarithmic spiral an ‘equiangular spiral’.

The logarithmic spiral is one of the most bewitching curves in maths. In the seventeenth century Jakob Bernoulli was the first mathematician to investigate its properties thoroughly. He called it the
spira mirabilis
, the wonderful spiral. He asked to have one engraved on his tombstone, but the sculptor engraved an Archimedean spiral by mistake.

The fundamental property of the logarithmic spiral is that it never changes shape the more it grows. Bernoulli expressed this on his tombstone with the epitaph:
Eadem mutata resurgo
, or ‘Although changed, I shall arise the same’. The spiral rotates an infinite number of times before reaching its pole. If you took a microscope and looked at the centre of a logarithmic spiral, you would see the same shape that you would see if the logarithmic spiral above was continued until it was as big as a galaxy and you were looking at it from a different solar system. In fact, many galaxies are in the shape of logarithmic spirals. Just like a fractal, a logarithmic spiral is self-similar, that is, any smaller piece of a larger spiral has identical shape to the larger piece.

The most stunning example of a logarithmic spiral in nature is the nautilus shell. As the shell grows, each successive chamber is larger, but has the same shape as the chamber before. The only spiral that can accommodate chambers of different sizes with the same relative dimensions is Bernoulli’s
spira mirabilis
/span>.

As Descartes noted, a straight line from the pole of a logarithmic spiral always cuts the curve at the same angle, and this feature explains why the spiral is used by Peregrine falcons when they attack their prey. Peregrines do not swoop in a straight line, but rather bear down on prey by spiralling around it. In 2000 Vance Tucker of Duke University figured out why this is so. Falcons have eyes at the sides of their head, which means that if they want to look in front of themselves, they need to turn their head 40 degrees. Vance tested falcons in a wind tunnel and showed that with their head at such an angle, the wind drag on a falcon is 50 percent greater than it would be if they were looking straight ahead. The path that lets the bird keep its head in the most aerodynamic position possible, while also enabling it to constantly look at the prey at the same angle, is a logarithmic spiral.

Nautilus shell.

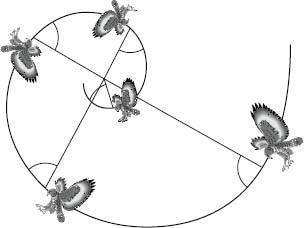
Falcons descend on their prey in a logarithmic spiral.

Plants, as well as birds of prey, move to the music of phi. When a plant grows, it needs to position its leaves around the stem in such a way as to maximize the amount of sunlight that falls on each leaf. That’s why plant leaves aren’t directly above each other; if that were the case, the bottom ones would get no sunlight at all.

As the stem goes higher, each new leaf appears at a fixed angle around the stem from the previous leaf. The stem sprouts a leaf at a predetermined rotation, as in the diagram on the following page.

What is the fixed angle that maximizes sunlight for the leaves, the angle that will spread out the leaves around the stem so that they overlap as little as possible? It is not 180 degrees, or a half turn, because the third leaf would be directly above the first. The angle is not 90 degrees, or a quarter turn, because if this were the case, the fifth leaf would be directly over the first – and also the first three leaves would be using only one side of the stem, which would be a waste of the sunlight available on the other side. The angle that provides the best arrangement is 137.5 degrees, and the diagram above shows where the leaves would be positioned if successive leaves are always separated by this angle. The first three leaves are positioned well apart from each other. The next two, leaves four and five, are separated by more than 50 degrees from their nearest leaves, which still gives them a good amount of room. The sixth leaf is at 32.5 degrees from the first. This is closer to a leaf than any previous one, which it has to be since there are more leaves, yet the distance is still a pretty wide berth.

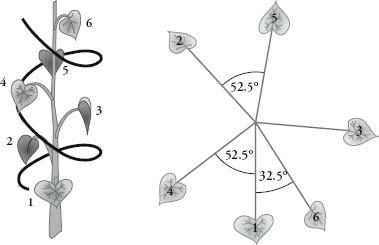
How leaves spiral up a stem.

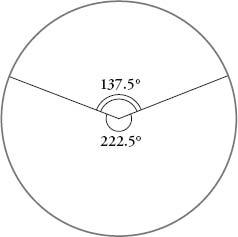
The angle of 137.5 degrees is known as the golden angle. It is the angle we get when we divide the full rotation of a circle according to the golden ratio. In other words when we divide 360 degrees into two angles such that the ratio of the larger angle to the smaller angle is phi, or 1.618. The two angles are 222.5 degrees and 137.5 degrees, to one decimal place. The smaller one is known as the golden angle.

The mathematical reason why the golden angle produces the best leaf arrangement around a stem is linked to the concept of irrational numbers, which a those numbers that cannot be expressed as fractions. If an angle is an irrational number, no matter how many times you turn it around a circle you will never get back to where you started. It may sound Orwellian, but some irrational numbers are more irrational than others. And no number is more irrational than the golden ratio. (There’s a brief explanation why in the
appendix
.)