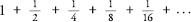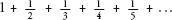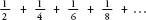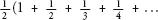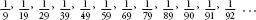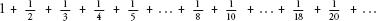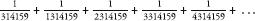Alex’s Adventures in Numberland (50 page)

For example, we have already seen that the series

is convergent, and converges on 2. We have also seen that there are many infinite series that converge on pi.

On the other hand, the series

is divergent, heading off towards infinity.

The Greeks may have been wary of infinity, but by the seventeenth century mathematicians were happy to take it on. An understanding of infinite series was required for Isaac Newton to invent calculus, which was one of the most significant developments in mathematics.

When I studied maths one of my favourite exercises was being presented with an infinite series and being asked to work out whether it converged or diverged. I always found it incredible that the difference between convergence and divergence was so brutal – the difference between a finite number and infinity is infinity – and yet the elements that decided which path the series took often seemed so insignificant.

Take a look at the
harmonic series
:

The nominator of every term is one, and the denominators are the natural numbers. The harmonic series looks like it should converge. Each term in the series gets smaller and smaller, so you would think that the sum of all the terms would be bounded by a fixed amount. But, bizarrely, the harmonic series is divergent, a decelerating but unstoppable snail. After 100 terms of the series, the total has only just passed 5. After 15,092,688,622,113,788,323,693,563,264,538, 101,449,859,497 terms, the total exceeds 100 for the first time. Yet this stubborn snail will continue its bid for freedom, past any distance you care to mark out. The series will eventually reach a million, then a billion, going further and further towards infinity. (The proof is included as an
appendix
.)

The harmonic series appears when we consider the maths of stacking Jenga blocks. Say you have two blocks and want to position them one on top of the other so that the top one has the largest possible overhang, but doesn’t topple over. The way to do this is to place the top block exactly halfway across the one underneath, as demonstrated opposite (A). In this way, the centre of gravity of the top block falls on the edge of the bottom brick.

If we had three blocks, what would be their positions so the combined overhang was as large as possible without toppling? The solution is for the top one to be placed halfway along the middle one, and for the middle one to be a quarter of the way along the bottom one, as in the diagram opposite (B).

Continuing for more and more blocks, the general pattern is that, in order to guarantee the maximum combined overhang, the top one must be halfway along the second one, which must be a quarter along the third one, which must be a sixth along the fourth one, which must be an eighth along the fifth one, and so on. This gives us a leaning tower of bricks that looks like C on the page opposite.

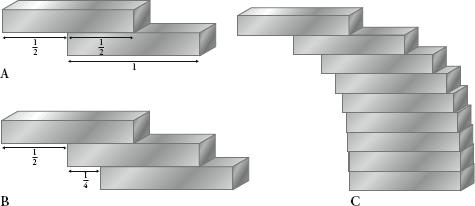
How to stack Jenga blocks with maximum overhang so that they don’t topple.

The total overhang of this tower, which is the sum of all the individual overhangs, is the following series:

Which can be rewritten as:

Which is half of the harmonic series, if we carry on for an infinite number of terms.

Now, since we know that the harmonic series increases to infinity, we also know that the harmonic series divided by two increases to infinity, because infinity divided by two is infinity. Rephrased in the context of stacking Jenga blocks, this means that it is theoretically possible to create a freestanding overhang of any length we want. If the harmonic series divided by two will eventually exceed any number we want, provided we include enough terms, then the overhang of the leaning tower of blocks will eventually exceed any length we want, provided we stack enough blocks. Although theoretically possible, however, the practicalities of constructing a tower with a large overhang are daunting. In order to achieve an overhang of 50 blocks, we would need a tower of 15×10
⁴²
blocks – which would be much higher than the distance from here to the edge of the observable universe.

The delights of the harmonic series are profuse, so let’s have some more fun with it. Consider the harmonic series
excluding
every term that has a 9 in it, which is also an infinite series. In other words, we are extracting the following terms:

So, the depleted series looks like:

Recall that the harmonic series adds up to infinity, so one might think that the harmonic series with no 9s also adds up to a pretty high number. Wrong. It adds up to just under 23.

By filtering out 9 we have tamed infinity: we have slaughtered the beast of eternity and all that is left is a shrivelled carcass of about 23.

This result appears remarkable, but by looking a little closer we can understand it completely. Eliminating a 9 gets rid of only one of the first 10 terms of the harmonic series. But it gets rid of 19 of the first 100 terms, and 271 of the first thousand. By the time the numbers are very large, sayrhang are100 digits, the vast majority of numbers contain a 9. As it turns out, thinning the harmonic series by taking out the terms with a 9 removes almost all of it.

Customizing the harmonic series gets more intriguing than this, though. The decision to extract 9s was arbitrary. If I had extracted all the terms containing 8 from the harmonic series, the remaining terms would also converge to a finite number. As it would if I extracted only the terms with a 7, or indeed with any single digit. In fact, we do not even need to limit ourselves to single digits. Remove all terms including
any
number, and the thinned-out harmonic series is convergent. This works with, say, 9 or 42 or 666 or 314159, and the same reasoning applies.

I’ll use the example of 666. Between 1 and 1000 the number 666 occurs once. Between 1 and 10,000 it occurs 20 times, and between 1 and 100,000 it occurs 300 times. In other words, the percentage occurrence of 666 is 0.1 percent in the first 1000 numbers, 0.2 percent in the first 10,000 and 0.3 percent in the first 100,000. As you consider larger and larger numbers, the string of digits 666 is proportionately more and more common. It will eventually be the case that almost all numbers have a 666 in them. So, almost all terms in the harmonic series will eventually have a 666 in them. Exclude them from the harmonic series and the depleted series converges.

In 2008 Thomas Schmelzer and Robert Baillie calculated that the harmonic series without any term containing the number 314159 adds up to a little over 2.3 million. It is a large number, but a long, long way from infinity.

A corollary of this result is that the harmonic series with
only
the terms including 314159 must add up to infinity. In other words, the series: