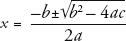Alex’s Adventures in Numberland (37 page)

Whereas the logarithm was a brand-new invention made possible by advances in notation, the
quadratic equation
was an ancient mathematical staple that was spruced up by new symbology. In modern notation, we say that a quadratic equation is one that looks like this:

Quadratics, in other words, are equations with an
x
and an
x
2. They occur most basically in calculations involving area. Consider the following problem from a Babylonian clay tablet: a rectangular field with area 60 units has one side that is 7 units bigger than the other. How big are the sides of the field? To find the answer we need to sketch the problem, as in the diagram below. The problem reduces to solving the quadratic equation
x
2 + 7
x
– 60 = 0.

A convenient feature of quadratic equations is that they can be solved by substituting the values for
a
,
b
and
c
in this one-size-fits-all formula:

The ± means that there are two solutions, one for the formula with a + and one with a –. In the Babylonian problem,
a
= 1,
b
= 7 ad
c
= –60, which gives the two solutions 5 and –12. The negative solution is meaningless when describing area, so the answer is 5.

Quadratics are used in calculations other than those analysing area. Physics was essentially born with Galileo Galilei’s theory of falling bodies, which he supposedly discovered by dropping cannonballs from the Leaning Tower of Pisa. The formula he derived to describe the distance of a falling object was a quadratic equation. Since then, quadratics have become so crucial to the understanding of the world that it is no exaggeration to say that they underpin modern science.

Even so, not every problem can be reduced to equations in
x
2. Some require the next power of
x
up the scale:
x
3. These are called
cubic
equations, and are of the form:

Cubic equations often emerge with calculations involving volumes, in which one may need to multiply the three dimensions of a solid object. Even though they are just one level up from quadratics, cubic equations are much more difficult to solve. Whereas the quadratic was cracked thousands of years ago – the Babylonians, for example, were able to solve them before algebra had been invented – at the beginning of the sixteenth century, the cubic was still beyond the abilities of mathematicians. All that would change in the year 1535.

In Renaissance Italy the unknown quantity, or
x
, was called the
cosa
, or ‘thing’. The science of equations was known as the ‘cossick art’, and the specialist professionals who solved them were ‘cossists’, literally, ‘thingists’. The thingists were not just ivory-tower academics, but also tradesmen who hired out their mathematical skills to a burgeoning commercial class that needed help with sums. Dealing in unknowns was a competitive business, and like master craftsmen, cossists kept their best techniques close to their chests.

Despite their secrecy, however, in 1535 a rumour circulated through Bologna that two cossists had discovered how to solve the cubic equation. For the cossick community, the news was pretty damn exciting. Conquering the cubic would elevate an equation professional above his peers and allow him to charge higher rates.

In modern academia the announcement of the proof of a famous unsolved problem would be presented through the publication of a paper, perhaps at a press conference, but back in the Renaissance the thingists agreed to a public mathematical duel.

On 13 February crowds gathered at the University of Bologna to see Niccolò Tartaglia and Antonio Fiore fight it out. The rules of the contest were that each man would challenge the other with 30 cubic equations. For each equation solved correctly, the solver would win a banquet paid for by his opponent.

The contest ended in a knockout victory for Tartaglia. (His name translates as ‘Stammerer’, and was a nickname he gained thanks to a sabre wound that had left him facially disfiured and with a severe speech impediment.) Tartaglia solved all of Fiore’s problems in two hours, while Fiore was unable to solve even one of Tartaglia’s. As the first person to discover a method of solving cubic equations, Tartaglia was the envy of mathematicians across Europe, but he wouldn’t tell anyone how he did it. In particular, he resisted the entreaties of Girolamo Cardano, who was probably history’s most colourful mathematician of significance.

Cardano was a doctor by profession, and he was internationally known for his cures – he once travelled to Scotland to treat the asthma of the country’s archbishop. He was also a prolific writer. In his autobiography he lists 131 printed books, 111 unprinted books, and 170 manuscripts he rejected himself as not good enough.
Consolation
, his compendium of advice to the sorrowful, was a bestseller throughout Europe, and is understood by literary scholars to be the book that Hamlet has in his hands during his ‘to be or not to be’ soliloquy. He was also a professional astrologer and claimed to have invented ‘metoposcopy’, the reading of character from the irregularities of one’s face. In mathematics, Cardano’s major contribution was the invention of probability, which I will return to later.

Cardano was desperate to know how Tartaglia had solved the cubic equation, so wrote to him, asking if he could include his cubic solution in a book he was writing. When Tartaglia refused, Cardano asked again, this time promising that he wouldn’t tell anyone else. Again, Tartaglia refused.

Extracting the cubic formula from Tartaglia became an obsession of Cardano’s. He eventually thought up a ruse – he invited Tartaglia to Milan on the pretext of setting up an introduction to a potential benefactor, the governor of Lombardy. Tartaglia accepted the offer, but once he arrived, discovered that the governor was out of town. Instead, he encountered only Cardano. Worn out from Cardano’s incessant pestering, Tartaglia relented, telling Cardano that if he could keep the formula to himself, he would reveal it to him. But when he passed over the information to Cardano, the crafty Tartaglia wrote the solution in a deliberately abstruse way: as a bizarre poem of 25 lines.

Despite this impediment, the multi-talented Cardano deciphered the method, and he almost kept his promise. He told the solution to only one person, his personal secretary, a young boy named Lodovico Ferrari. This turned out to be problematic, not because Ferrari was indiscreet, but because he improved on Tartaglia’s method to find a way to solve
quartic equations
. These are equations that require the power of
x
⁴
. For example, 5
x
⁴
– 2
x
³
– 8
x
²
+ 6
x
+ 3 = 0. A quartic may arise when multiplying one quadratic with another.

Cardano was in a fix – he couldn’t publish Ferrari’s discovery without betraying Tartaglia’s word, but neither could he deny Ferrari the public acclamation that he deserved. Cardano, however, managed to find a clever way out. It turned out that Antonio Fiore, the man who lost the cubic duel against Tartaglia, did in fact know how to solve the cubic, and he had learned the method from an older mathematician, Scipione del Ferro, who had told Fiore from his deathbed. Cardano discovered this after approaching del Ferro’s family and going through the late mathematician’s unpublished notes. Cardano thus felt morally justified in publishing the result, crediting del Ferro as the original inventor, and Tartaglia as the reinventor. The method was included in Cardano’s
Ars Magna
, the most important book on algebra of the sixteenth century.

Tartaglia never forgave Cardano, and died an angry and bitter man. Cardano, however, lived until he was nearly 75. He died on 21 September 1576, the date he had predicted when casting his horoscope years before. Some maths historians claim he was in perfect health and drank poison just to ensure his prediction would come true.

Rather than just looking at equations with higher and higher powers of
x
, we can also increase complexity by adding a second unknown number,
y
. The school algebra favourite that is known as
simultaneous equations
is usually the task of solving two equations that each have two variables. For example:

y
=
x

y
= 3
x
– 2

To solve the two equations, we substitute the value of the variable in one equation with the value from the other. In this case, since
y
=
x
, then:

x
= 3
x
– 2

Which reduces to 2
x
= 2

So
x
= 1, and
y
= 1

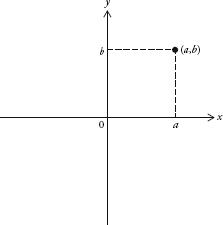
It’s also possible to understand any equation in two variables visually. Draw a horizontal line and a vertical line that intersect. Define the horizontal line as the
x
-axis, and the vertical line as the
y
-axis. The axes intersect at 0. The position of any point in the plane can be determined by referencing a point on both axes. The position (
a,b
) is defined as the intersection of a vertical line through
a
on the
x
-axis and a horizontal line through
b
on the
y
-axis.