Alex’s Adventures in Numberland (41 page)

But the effort was worth it, and in September 2004 he persuaded New Hampshire’s
Conway Daily Sun
to publish one of his puzzles. It was an immediate success. The following month he decided to approach the British national press. Gould thought the most effective way to pitch his idea was to present a mock-up of that day’s paper with the Sudoku already in it. He knew enough about forgery from covering trials in Hong Kong to make a convincing fake of
The Times
’s second section, and took it to the paper’s head office. After waiting a few hours in reception, Gould showed them his dummy paper, and they seemed to like it. In fact, immediately after he left, a
Times
executive sent Gould an email asking him not to show the Sudoku puzzles to anyone else. Two weeks later the puzzle first appeared, and three days after that, the
Daily Mail
introduced its own version. In January 2005 the
Daily Telegraph
joined the game, and not long afterwards every British newspaper had to have a daily puzzle to keep up with the competition. That same year the
Independent
reported a 700 percent rise in UK pencil sales, and attributed it to the craze. By summer, shelves of Sudoku books appeared in bookshops, newsagents and airports, and not just in the UK but around the world. At one point in 2005 six of the top 50 books on
USA Today
’s bestseller list were Sudoku titles. By the end of the year the puzzle had spread to 30 countries, and
Time
magazine named Wayne Gould one of the 100 people who most shaped the world that year, along with Bill Gates, Oprah Winfrey and George Clooney. By the end of 2006, Sudokus were being published in 60 countries; and by the end of 2007, in 90. According to Maki Kaji, the number of regular Sudoku players now exceeds 100 million people.

Completing any puzzle is immensely gratifying to the ego, but part of the extra allure of completing a Sudoku is the inner beauty and balance of the perfect Latin square that gives it its form. Sudoku’s success is testament to an age-old, cross-cultural fetish for number squares. And unlike many other puzzles, its success is also a remarkable victory for mathematics. The puzzle is maths by stealth. Although Sudoku contains no arithmetic, it does require abstract thought, pattern recognition, logical deduction and the generation of algorithms. The puzzle also encourages an aggressive attitude towards problem-solving, and fosters an appreciation of mathematical elegance.

For instance, as soon as you understand the rules of Sudoku, the concept of a
unique solution
is remarkably clear. For every pattern of numbers in the grid at the start, there is only one possible final arrangement for the numbers in the empty spaces. However, it is not the case that every partially filled grid has a unique solution. It is perfectly possible that a 9 × 9 square with some numbers filled in has no solutions, just as it is perfectly possible that it has many solutions. When Sky TV launched a Sudoku show, they drew what they claimed was the world’s largest Sudoku by cutting a 275 × 275ft grid out of a chalk hillside in the English countryside. However, the given numbers were placed in such a way that there were 1905 valid ways to complete the square. The roclaimed largest Sudoku did not have a unique solution, and therefore was not a Sudoku at all.

The branch of mathematics that involves the counting of combinations, such as all the 1905 solutions to Sky TV’s faux Sudoku, is called
combinatorics
. It is the study of permutations and combinations of things, such as grids of numbers, but also, famously, the schedules of travelling salesmen. Let’s say, for instance, that I’m a travelling salesman and I have 20 shops to visit. In what order should I visit them so that my total distance is the shortest? The solution requires me to consider all the permutations of paths between all the shops, and is a classic (and extremely difficult) combinatorial problem. Similar problems arise throughout business and industry, for example in scheduling flight departure times at airports or having an efficient postal sorting system.

Combinatorics is the branch of maths that most consistently deals with extremely high numbers. As we saw with magic squares, a small set of numbers can be rearranged in an astonishingly large number of ways. Though they both share square grids, there are fewer Latin squares than magic squares for the same size of grid, though the number of Latin squares is still colossal. The number, for example, of 9 × 9 Latin squares is 28 digits long.

How many possible Sudokus are there? If a 9 × 9 Latin square is to qualify as a finished Sudoku grid, the 9 subsquares must also include every digit, and this reduces the total of Sudoku-ready 9 × 9 squares to 6,670,903,752,021,072,963,960. Many of these grids, however, are different versions of the same square when reflected or rotated (as I showed with the 3 × 3 magic square on chapter 6). Eliminating squares that are rotations and reflections, the number of distinct possible finished Sudoku grids is about 5.5 billion.

Still, this is not the total number of possible Sudokus, which is much larger since each finished grid will be the solution to many Sudokus. For example, a Sudoku in a newspaper has one unique solution. Once you fill in one of the squares, however, you are creating a new grid with a new set of givens, in other words a new Sudoku with the same unique solution, and so on for each square you fill in. So if a Sudoku has, say, 30 given numbers, then we will be able to create another 50 Sudokus with the same unique solution until we complete the grid. (That’s one new Sudoku for each extra number, until there are 80 givens in the 81-square grid.) Finding the total number of Sudokus is not that interesting since what we will find is that most of these Sudokus have grids with very few blank spaces in them, which is not in the spirit of the puzzle. Instead, mathematicians get much more excited about the number of digits you can leave in the square. The number one combinatorics question about Sudoku is what is the least amount of numbers you can leave in the square so that there is only one way to fill in the grid?

The Sudokus published in newspapers usually include around 25 given numbers. To date, no one has found a Sudoku that has a unique solution with fewer givens than 17. In fact, 17-clue Sudokus inspire something of a combinatorics cult. Gordon Royle, of the University of Western Australia, maintains a database of 17-clue Sudokus, and receives three or four new ones every day from puzzle-makers around the world. So far, he has collected almost 50,000. But even though he is the world’s expert on 17-clue puzzles, he says he doesn’t know how close he is to finding the total number of possible puzzles. ‘A while ago I would have said that we were close to the end, but then an anonymous contributor sent in nearly 5000 new ones,’ he said. ‘We never really worked out how 8220;anon17” could do it, but it clearly involved a clever algorithm.’

In Royle’s opinion, no one has found a 16-clue Sudoku because, as he said, ‘Either we are not clever enough or our computers are not powerful enough.’ Most likely, anon17 didn’t reveal his method because he was using someone else’s very large computer when he wasn’t supposed to. Answering combinatorics problems often relies on giving the hard work of number-crunching over to a computer. ‘The total possible space of 16-clue possible puzzles is far too vast for us to explore more than a tiny proportion of it without some new theoretical ideas,’ Royle claimed. But he has a gut feeling that no 16-clue Sudokus will ever be found, adding: ‘We have so many 17-clue puzzles now it would really be a bit strange if there was a 16-clue puzzle that we had not stumbled across.’

Maki Kaji’s business card has the words
Godfather of Sudoku
. Wayne Gould describes himself as the Stepfather of Sudoku. I finally met up with Gould over coffee in a West London deli. He was wearing a New Zealand rugby top and had a typically antipodean, easygoing manner. Gould has a gap between his front teeth, which together with his thick glasses, short silvery hair and youthful enthusiasm reminded me of a young university lecturer rather than a former judge. Sudoku has transformed Gould’s life. He has been busier in retirement than he ever was before. He supplies puzzles for free to more than 700 newspapers in 81 countries, earning money from selling his program and books, which he says gives him only about 2 percent of the global Sudoku market. Still, Sudoku has earned him a seven-figure fortune. And he is a celebrity. When I asked him how his wife felt about his unexpected fame, he paused. ‘We separated last year,’ he stuttered. ‘After 32 years of marriage. Maybe it was having all that money. Maybe it gave her a freedom she never knew she had.’ Through the silence the message I heard was a heartbreaking one: he might have launched a global craze, but the adventure had come at too high a personal cost.

I’ve always thought that one reason for Sudoku’s success is its exotic name, which resonates with the romance of superior Oriental wisdom, despite the fact that the American Howard Garns came up with the idea in Indiana. In fact, there is a tradition of puzzles coming from the East. The very first international puzzle craze dates from the early nineteenth century, when European and American sailors returning from China brought home sets of geometrical shapes, typically made of wood or ivory, that had seven pieces – two large triangles, two small triangles, a medium-sized triangle, a rhomboid and a square. Put together, the pieces made up a larger square. Accompanying the sets were booklets with dozens of outlines of geometrical shapes, human figures and other objects. The aim of the puzzle was to use all seven of the pieces to create each printed silhouette.

The puzzle had originated with the Chinese tradition of arranging tables of different shapes for banquets. One Chinese book, from the twelfth century, showed 76 banquet placements, many of which were made to look like objects, such as a fluttering flag, a range of mountains and flowers. At the turn of the nineteenth century a Chinese writer with the playful nickname Dim-Witted Recluse adapted this ceremonial choreography for finger-sized geometrical blocks and put the figures in a book,
Pictures Using Seven Clever Pieces
.

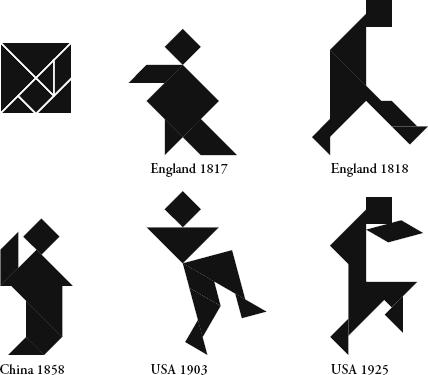
Tangram figures through the ages.

Originally called the Chinese Puzzle, the sets later gained the name ‘tangram’. The first book of tangram puzzles to be published outside China was printed in London in 1817. Immediately, the book started a fad. Between 1817 and 1818 dozens of tangram books came out in France, Germany, Italy, the Netherlands and Scandinavia. Cartoonists of the day captured the craze by portraying men unwilling to go to bed with their wives, chefs unable to do the cooking and doctors refusing to attend patients because they were too busy rearranging triangles. The craze was more pronounced in France, perhaps because one of the books claimed that the puzzle was Napoleon’s favourite amusement during his exile on the South Atlantic island of St Helena. The former emperor was an early adopter since ships stopped off there on their way back from Asia.

I love the tangram. Men, women and animals magically come to life. By a slight repositioning of just one piece the personality of the figure changes entirely. With their angular and often grotesque contours, the figures are wonderfully suggestive. The French took this personification to an extreme by actually painting images within the silhouettes.

It is hard to believe how engrossing the puzzle is until you have tried it out. In fact, though it looks easy, solving tangram problems can be surprisingly difficult. The shapes can easily deceive, as when two similar-looking silhouettes have totally different underlying structures. The tangram can serve as a warning against complacency, reminding you that the essence of objects may not always be what you first see. Take a look at the following tangram figures. It looks as if a small triangle has been removed from the first to make the second. In fact, both figures use all the pieces and they are arranged in completely different ways.