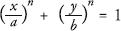Alex’s Adventures in Numberland (39 page)

In downtown Stockholm there is a main public plaza called Sergels Torg. It’s a large rectangular space, with a pedestrian lower level and a traffic circle on top. It’s the place activists choose to hold political rallies, and where sports fans congregate when Sweden’s national teams win a major event. The plaza’s dominant feature is a cetral section with a sturdy 1960s sculpture that locals love to hate – a 37m-high glass and steel obelisk that lights up at night.

During the late 1950s, when city planners were designing Sergels Torg, they encountered a geometrical problem. What, they asked themselves, is the best shape for a roundabout in a rectangular space? They didn’t want to use a circle because that would not use the rectangular space fully. But nor did they want to use an oval or an ellipse – which do fill the space – because the pointed ends of either shape would hinder the smooth flow of traffic. Searching for an answer, the architects on the project looked abroad, and consulted Piet Hein, a man once described as the third-most famous person in Denmark (after the physicist Niels Bohr and the writer Karen Blixen). Piet Hein was the inventor of the grook, a style of short aphoristic poem that he published in Denmark during the Second World War as a form of passive resistance against Nazi occupation. He was also a painter and mathematician, so possessed the right combination of artistic sensibilities, lateral thinking and scientific understanding to give fresh ideas to Scandinavian planning problems.

Piet Hein’s solution was to find a shape that was halfway between an ellipse and a rectangle, using simple mathematics. To achieve this, he used the method described on the previous page. He adjusted the exponent in the equation for the ellipse to get a shape that would fit inside the rectangular plaza at Sergels Torg. In algebraic terms, he did what Lamé did by playing around with the
n
in the ellipse equation:

As I showed previously, increasing the
n
from 2 to infinity takes you from a circle to a square, or from an ellipse to a rectangle. Piet Hein judged that the value of
n
such that the curve was the most aesthetic compromise between round and right-angled was when
n
= 2.5. He could have called his new shape a ‘squircle’. Instead, he called it a superellipse.

More than just an elegant piece of maths, Piet Hein’s superellipse touched on a deeper human theme – the ever-present conflict in our surroundings between circles and straight lines. As he wrote, ‘In the whole pattern of civilization there have been two tendencies, one toward straight lines and rectangular patterns and one toward circular lines.’ His piece continued, ‘There are reasons, mechanical and psychological, for both tendencies. Things made with straight lines fit well together and save space. And we can move easily – physically or mentally – around things made with round lines. But we are in a straitjacket, having to accept one or the other, when often some intermediate form would be better. The superellipse solved the problem. It is neither round nor rectangular, but in between. Yet it is fixed, it is definite – it has a unity.’

Stockholm’s superelliptical roundabout was copied by other architects, most notably in the design for the Azteca stadium in Mexico City – which held the World Cup final in 1970 and 1986. In fact, Piet Hein’s curve spread to fashion, becoming a feature of 1970s Scandinavian furniture design. It’s still possible to buy superelliptic plates, trays and door-handles from the company run by Piet Hein’s son.

Piet Hein’s playful mind did not stop at the superellipse, however. F his next project, he wondered what a three-dimensional version of the shape would look like. The result was halfway between a sphere and a box. He could have called it a ‘sphox’. Instead, he called it a ‘superegg’.

Supereggstatic: Uri Geller.

One unexpected feature of the superegg was that it could stand on its end without falling. In the 1970s Piet Hein marketed super-eggs made out of stainless steel as a ‘sculpture, novelty or a charm’. They are beautiful, curious objects. I have one on my mantelpiece. Uri Geller also has one. John Lennon gave it to him, explaining that he had received the egg from aliens who visited him in his New York apartment. ‘Keep it,’ Lennon told Geller. ‘It’s too weird for me. If it’s my ticket to another planet, I don’t want to go there.’

Maki Kaji runs a Japanese magazine that specializes in number puzzles. Kaji considers himself an entertainer who uses numbers as the tools of his trade. ‘I feel more like a film or theatre director than a mathematician,’ he explained. I met Kaji at his office in Tokyo. He was neither geeky nor formal, two characteristics one might expect to find in a numbers guy-turned-successful businessman. Kaji was wearing a black T-shirt under a trendy beige cardigan, and a pair of John Lennon glasses. Aged 57, he has a trim white goatee and sideburns, and often grins effervescently. Kaji keenly told me about his other hobbies, besides number puzzles. For instance, he collects rubber bands, and on a recent trip to London found what to him amounted to a glorious cache – a 25g pack of branded rubber bands from WH Smith and a 100g pack from an independent stationer. He also amuses himself by photographing arithmetically gratifying car licence plates. In Japan, licence plates consist of two numbers followed by another two numbers. Kaji carries a small camera at all times and snaps every registration he sees for which the first pair multiplied by each other equals the second pair.

Assuming that no Japanese car has a 00 for the second pair of digits, each plate Kaji photographs is a line in the times tables of the digits 1 to 9. For instance, 11 01 can be thought of as 1×1 = 1. Likewise, 12 02 is 1×2 = 2. We can carry on the list, and work out that there are 81 possible combinations. Kaji has already collected more than 50. Once he has gathered the full set of times tables, he plans to exhibit them in a gallery.

The idea that numbers can entertain is as old as maths itself. The ancient Egyptian Rhind Papyrus, for example, contains the following list as part of the answer to problem 79. Unlike the other problems in the papyrus, this one has no apparent practical application.

Kaji snaps 3
×
5 = 15 in a Tokyo car park.

The list is the inventory of seven houses, each of which had seven cats, each of which ate seven mice, each of which ate seven grains of spelt, each of which came from a separate
hekat
. The numbers form a
geometric progression
– which is a sequence where each term is calculated by multiplying the previous term by a fixed number, in this case, seven. There are seven times more cats than houses, seven times more mice than cats, seven times more grains of spelt than mice, and seven times more
hekats
than grains of spelt. We could rewrite the total number of items as 7 + 7
²
+ 7
³
+ 7
⁴
+ 7
⁵
.

It wasn’t just the Egyptians, however, who found such a sequence irresistible. Almost exactly the same sum reappeared in the early nineteenth century in a Mother Goose nursery rhyme:

The verse is the most famous trick question in English literature since, presumably, the man and his phalanx of females and confined felines were coming
from
St Ives. Irrespective of the direction of travel, however, the total number of kits, cats, sacks and wives is 7 + 7
²
+ 7
³
+ 7
⁴
, which is 2800.

Another, less well-known, appearance of the riddle is as a problem in Leonardo Fibonacci’s
Liber Abaci
, from the thirteenth century. This version involved seven women on their way to Rome with increasing numbers of mules, sacks, loaves, knives and sheaths. The extra 7
⁶
brings the series to 137,256.

What is the allure of rising powers of seven that they have appeared in such different ages and contexts? Each case demonstrates the turbo-charged acceleration of geometric progressions. The rhyme is a poetic way of showing how quickly small numbers can lead to big ones. On first hearing, you think there might be a fair amount kits, cats, sacks and wives – but not almost 3000 of them! Likewise, the playful problems set in the Rhind Papyrus and the
Liber Abaci
express the same mathematical insight. And the number 7, though it would seem like it should have some special quality to make it so common across these problems, is rather irrelevant. When you multiply any number by itself a few times, the sum quickly reaches a counter-intuitively high amount.

Even when multiplying the lowest number possible, 2, by itself, the sum swirls to the heavens at a dizzying pace. Place one grain of wheat on the corner square of a chessboard. Place two grains on the adjacent square, and then start filling up the rest of the board by doubling the grains of wheat per square. How much wheat would you need to fill the final square? A few truckloads, or a container, maybe? There are 64 squares on a chessboard, so we have doubled up 63 times, meaning that the number is 2 multiplied by itself 63 times, or 2
⁶³
. In grains, this number is about 100 times more than the world’s current annual wheat production. Or, to consider it another way, if you started counting a grain of wheat per second at the very moment of the Big Bang 13 billion or so years ago, then you would not even have counted up to a tenth of 2
⁶³
by now.

Mathematical riddles, rhymes and games are now collectively known as
recreational maths
. It is a wide-ranging and vibrant field, an essential feature of which is that the topics are accessible to the dedicated layperson, even though they might touch on impossibly complicated theory. Or they might not even involve theory at all, but rather merely kindle an appreciation of the wonder of numbers – such as the thrill of collecting pictures of licence plates.

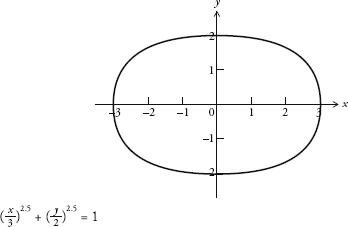
A landmark event in the history of recreational maths is said to have taken place by the banks of the Yellow River in China around 2000 bc. According to legend, Emperor Yu saw a turtle creep out of the water. It was a divine turtle, with black and white dots on its underbelly. The dots denoted the first nine numbers and formed a grid on the turtle’s belly that (if the dots were instead written as Arabic numerals) looked like A:

A square like this one, that contains all the consecutive numbers starting from 1 and arranged so that all the rows, columns and corner-to-corner diagonals add up to the same total, is known as a
magic square
. The Chinese called this square the
lo shu
. (Its rows, columns and diagonals all add up to 15.) The Chinese believed that the
lo shu
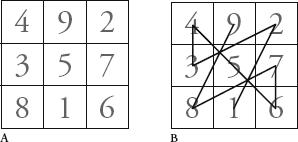
symbolized the inner harmonies of the universe and used it for divination and worship. For example, if you start at 1 and draw a line between the numbers of the square in order, you map out the pattern that can be seen in B and the figure opposite, which shows the instructions for the movement of Taoist priests through a temple. The pattern, which is called the
yubu
, also underlies some of the rules of
feng shui
, the Chinese philosophy of aesthetics.

Taoist woodblock print with the yubu.

China was not the only culture to see the mystical side of the
lo shu
. Magic squares have been objects of spiritual importance for Hindus, Muslims, Jews and Christians. Islamic culture found the most creative uses. In Turkey and India vgins were required to embroider magic squares on the shirts of warriors. And if a magic square were placed over the womb of a woman in labour, it was believed that the birth would be an easier one. Hindus wore amulets with magic squares as protective charms, and Renaissance astrologers associated them with the planets in our solar system. It is easy to mock a predisposition for the occult in our ancestors, yet modern man can understand their fascination with magic squares. Both simple and yet subtly complex, a magic square is like a numerical mantra, an object of endless contemplation and a self-contained expression of order in a disordered world.

Melencolia I:
Dürer’s famous woodcut shows an angel lost in thought surrounded by mathematical and scientific objects, such as a compass, a sphere, a set of scales, an hourglass and a magic square. Art historians, especially those with a mystical bent, have long pondered the symbolism of the geometrical object in the middle left of the image, which is known as ‘Dürer’s solid’ mathematicians have long pondered the mystery of how on earth to construct it.

One of the pleasures of magic squares is that they are not restricted to 3 × 3 grids. A famous example of a 4 × 4 square comes from the work of Albrecht Dürer. In
Melencolia I
(shown opposite), Dürer included a 4 ×4 square that is best known for containing the year in which he engraved it: 1514.

Dürer’s square, in fact, is übermagic. Not only do the rows, columns and diagonals add up to 34, but so do the combinations of four numbers marked by dots and linked in the squares below.

The patterns Dürer’s square produces are amazing, and the more you look, the more you find. For example, the sum of the squares of the numbers on the first and second rows adds up to 748. You get the same total by adding up the squares of the numbers in rows 3 and 4, or the squares of the numbers in rows 1 and 3, or the squares of the numbers in rows 2 and 4, or the squares of the numbers in both diagonals. Wow!