Alex’s Adventures in Numberland (43 page)

In the mid nineteenth century American newspapers started to print chess problems. One of the first, and most precocious, devisers of these problems was Sam Loyd. A New Yorker, Loyd was just 14 when he had his first conundrum printed in a local paper. By 17 he was the most successful and widely celebrated deviser of chess problems in the US.

He moved on from chess to mathematically based puzzles, and by the end of the century was the world’s first professional puzzle-compiler and impresario. He published widely in the American media, and once claimed that his columns attracted 100,000 letters a day. However, we should take his figure with a pinch of salt. Loyd cultivated the kind of playful attitude towards the truth that one expects of a professional riddler. For a start, he claimed he had invented the Fifteen puzzle, which was taken to be true for more than a century until in 2006 historians Jerry Slocum and Dic Sonneveld properly traced its origin to Noyes Chapman. Loyd also revived interest in the tangram with
The 8th Book of Tan Part I
, a version of an ancient text about the supposed 4000-year history of the puzzle. The book was a spoof, even though it was initially taken seriously by academics.

Loyd had a unique brilliance at turning mathematical problems into entertaining, distinctively illustrated puzzles. His most genial creation was invented for the
Brooklyn Daily Eagle
in 1896. The ‘Get off the Earth’ puzzle widely i popular that it was later adopted as a publicity gimmick by several brands, including
The Young Ladies Home Journal
, the Great Atlantic & Pacific Tea Company and the Republican platform for the 1896 presidential election. (Although its message was not a manifesto pledge.) The puzzle is an image of Chinese warriors positioned around the Earth, which is on a disc made out of card that can be spun around its centre. When the arrow is pointing NE there are 13 warriors, but turn the disc so the arrow points NW and there are only 12. The puzzle is confusing. There really are 13 warriors, then – in a flash – just 12. Which man has vanished and where does he go?

The trick operating in this puzzle is known as a geometrical vanish. It can also be demonstrated in the following way. The image on chapter 6 shows a piece of paper with ten vertical lines on it. When the piece of paper is cut along the diagonal line, the two sections can be realigned so that only nine lines are created. Where has the tenth line gone? What has happened is that the segments have been rearranged to form nine lines that are
longer
than the original line. If the lines in the first image have the length 10 units, then the length of the lines in the second image is 11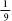
, since one of the original lines has been equally shared among the nine others.

What Sam Loyd did with ‘Get off the Earth’ is to curve the geometrical vanish so it was in a circular form, and in place of lines put Chinese warriors. There are 12 positions in his puzzle, akin to the 10 lines in the example overleaf. The position in the bottom left corner, where there are originally two warriors, is equivalent to the end lines of the vanish. When the arrow is moved from NE to NW, all the positions gain a bit more warrior, apart from the position with two warriors, which shrinks drastically, giving the impression that a whole warrior has been lost. In fact, it has just been redistributed around the others. Sam Loyd claimed that ten million copies of ‘Get off the Earth’ were produced. He became rich and famous, revelling in his reputation as the puzzle king of America.

Geometrical vanish: ten lines become nine.

Meanwhile, in Great Britain, Henry Ernest Dudeney was acquiring a similar reputation. If Loyd’s capitalist chutzpah and gift for self-publicity reflected the cut-and-thrust of turn-of-the-century New York, Dudeney embodied the more reserved English way of life.

From a family of Sussex sheep farmers, Dudeney started working at 13 as a clerk in the civil service in London. Bored with the job, he began to submit short stories and puzzles to various publications. Eventually he was able to devote himself to journalism full time. His wife Alice wrote bestselling romantic novels about life in rural Sussex – where, thanks to her royalties, the couple was able to live in luxury. The Dudeneys, dividing their time between the countryside and London, were part of a highbrow literary scene that included Sir Arthur Conan Doyle, the creator of Sherlock Holmes, probably the most iconic puzzle-solver in all literature.

It is thought that Dudeney and Sam Loyd first made contact in 1894, when Loyd posed a chess problem in the firm belief that no one would discover his 53-move solution. Dudeney, who was 17 years Loyd’s junior, found a solution in 50 moves. The men subsequently collaborated, but fell out when Dudeney discovered Loyd was plagiarizing his work. Dudeney despised Loyd so intensely that he equated him with the Devil.

While both Loyd and Dudeney were self-taught, Dudeney had a much finer mathematical mind. Many of his puzzles touched on deep problems – frequently predating academic interest. In 1962, for example, the mathematician Mei-Ko Kwan investigated a problem about the route a postman should take in a grid of streets so as to walk on every street and do it in the shortest route possible. Dudeney had framed – and solved – the same problem in a puzzle about a mine inspector walking through underground shafts almost 50 years earlier.

Dudeney also made unintended contributions to number theory. One of his puzzles, called
Root Extraction
, plays on the fact that the cube roots of the following numbers are also equal to the sum of the digits that make up those numbers:

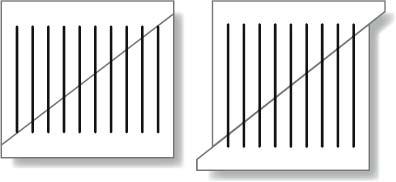
Numbers with this property – and there are only six of them – are now known as Dudeney numbers. Another particular forte of Dudeney’s was the geometrical dissection, which is when a shape is cut up into pieces and reassembled into another shape, like the principle behind the tangram. Dudeney found a way of converting a square into a pentagon in six pieces. His method became a popular classic because for many years it had been thought that the minimum dissection of a square into a pentagon required seven pieces.

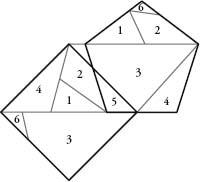
Dudeney also discovered a novel way to cut up a triangle and make it into a square in four pieces. And he realized that if the four pieces in his solution were hinged together, they could be assembled in a chain – such that folding one way gets you a triangle and folding the other way gets you the square. He called this the Haberdasher’s Puzzle, since the shapes look like the leftover pieces of cloth that a haberdasher might h in his shop. The puzzle thus introduced the concept of a ‘hinged dissection’, and aroused such interest that Dudeney made one out of mahogany with brass hinges and presented it in 1905 at a meeting of the Royal Society in London. The Haberdasher’s Puzzle was Dudeney’s greatest legacy and has fascinated and delighted mathematicians for more than a century.

The Haberdasher’s Puzzle.

One mind that was especially enthralled by the Haberdasher’s Puzzle belonged to the Canadian teenager Erik Demaine. Demaine, who was such a prodigy that by the time he was 20 he was already a professor at MIT, was most interested in the ‘universality’ of the problem. Is it possible, he wondered, to dissect
any
straight-sided shape and then hinge the pieces together in a chain so it can be folded into
any other
straight-sided shape of equal area? He spent ten years working on the problem and in March 2008, aged 27, announced the solution to a very receptive audience of puzzle-lovers in the ballroom of an Atlanta hotel.