Alex’s Adventures in Numberland (42 page)

In the mid nineteenth century, tangrams were embraced by schools, though they still remained an adult pastime. The German company Richter rebranded the tangram as the
Kopfzerbrecher
, or brain-buster, and, due to the product’s success, introduced more than a dozen similar rearrangement puzzles with different shapes cut into different pieces. During the First World War, Richter puzzles became a much-loved diversion for troops stuck in the trenches. Demand was so great that another 18 puzzles were launched. One of them was called the
Schützengraben Geduldspiel
– the trench patience game – which contained military shapes such as a Zeppelin, a revolver and a grenade. Some of the figures were devised by soldiers, who had sent the ideas in from the front.

First World War advert for Lott’s brick puzzles.

Before the war, Richter had licensed its puzzles to the Lott’s Brick Company in the UK. It was not only German soldiers who spent their days on the front solving tangram spin-offs; a few miles away in the Allied trenches, the British were doing exactly the same.

As each generation has created new figures, the tangram has never really gone out of fashion in almost 200 years. You can still buy the puzzle in toyshops and bookstores. The stock of published outlines is now more than 5900.

Despite the association of the tangram with puzzles of this kind, it was not the world’s first rearrangement puzzle. In ancient Greece the similar
stomachion
divided a square into 14 pieces. (
Stomachi
means ‘stomach’, and the name is thought to be a result of the bellyache that the puzzle induced, although not from ingesting the pieces.) Archimedes wrote a treatise on the
stomachion
, only a fraction of which survives. Based on this fragment, it has been suggested that the treatise was an attempt to calculate the number of different ways the pieces of the
stomachion
could be positioned to make a perfect square. Only recently was this particular ancient problem solved. In 2003 the computer scientist Bill Cutler found that there are 536 ways (excluding solutions that are identical under rotation or reflection).

The
stomachion
, which is also known as the ‘loculus of Archimedes’.

Since the time of Archimedes a keen interest in recreational puzzles has been a trait shared by many mathematicians. ‘Man is never more ingenious than in the invention of games,’ said Gottfried Leibniz, for instance, whose love of peg solitaire resonated with his obsession with binary numbers: a hole either has a peg in it or it doesn’t, it is either a 1 or a 0. However, the most playful of the great mathematicians was Leonhard Euler, who, in order to crack an eighteenth-century brainteaser, invented a whole new branch of mathematics.

In Königsberg, the former Prussian capital that is now the Russian city of Kaliningrad, there used to be seven bridges that crossed the River Pregel. Locals wanted to know if it would be possible to make a journey across all seven bridges without crossing any bridge more than once.

To come up with a proof that a circuit of this kind was impossible, Euler created a graph in which each landmass was represented by a dot, or node, and each bridge by a line, or link. He worked out a theorem that related the number of links touching each node to whether it was possible to make a circuit of the graph, and in this case it was impossible.

The conceptual leap Euler made was to realize that what was important to solve the problem was not information about the exact position of the bridges, but how they were connected. The London Underground map borrows this idea: it is not geographically accurate, but is faithful to how the Tube lines are linked together. Euler’s theorem launched graph theory, and presaged the development of topology, a very rich area of maths that studies the properties of objects that do not change when the object is squeezed, twisted or stretched.

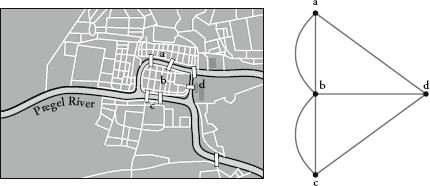
Königsberg in the eighteenth century: as a map and as a graph.

Fascination in 1817 with tangrams was nothing compared with the extraordinary levels of excitement generated by the world’s second international puzzle craze. From the day in December 1879 when the Fifteen puzzle launched in a Boston toyshop, manufacturers couldn’t meet the demand. ‘Neither the wrinkled front of age nor the cherubic brow of childhood is proof against the contagion,’ declared the
Boston Post
.

The Fifteen puzzle consisted of 15 square wooden blocks placed in a square carton so that the blocks made a × 4 square with one square missing. The blocks were numbered 1 to 15 and put in the box randomly. The aim of the puzzle was to slide the blocks around the 4 × 4 square using the empty space and finish with them positioned in numerical order. Playing with the Fifteen puzzle was so addictive and fun that the fad soon spread from Massachusetts to New York, and then across the United States. ‘It has swept over the land from East to West with the violence of the sirocco, scorching men’s brains as it passed, and apparently making them temporarily insane,’ quivered the
Chicago Tribune
. According to the
New York Times
, no pestilence ‘has ever visited this or any other country which has spread with [such] awful celerity’.

The puzzle soon went overseas, with one shop in London reportedly selling nothing else. Within six months it had reached the other side of the world. ‘Not a few have already been driven insane,’ claimed a letter in the
Otago Witness
, New Zealand, on 1 May 1880.

The Fifteen puzzle was initially known as the Gem puzzle.

The Fifteen puzzle was the creation of Noyes Chapman, a postmaster in upstate New York, who almost two decades previously had been trying to make a physical model of a 4 × 4 magic square. He made small wooden squares for each of the 16 numbers and fitted them snugly into a square box. When he realized that leaving out one block provided a space into which any adjacent block could be slid, he saw that trying to rearrange the numbers would make a particularly fun game. Chapman made a few versions for family and friends, but never capitalized on his invention. It was only when a savvy Boston carpenter decided to commercialize the puzzle that it finally took off.

The Fifteen puzzle was especially tormenting to those who attempted it because sometimes it was solvable and sometimes it was not. Once the blocks were randomly put in there seemed to be only two outcomes: either they could be rearranged in numerical order, or they could be rearranged so that the first three rows were in order but the last line went 13-15-14. The craze was fuelled, in part, by a desire to work out if it was possible to get from 13-15-14 to 13-14-15. In January 1890, a few weeks after the first puzzle went on sale, a dentist in Rochester, New York, placed an ad in the local paper offering a $100 prize and a set of false teeth to anyone who could prove it either way. He believed it was impossible – but needed some help with the maths.

Bafflement with the Fifteen puzzle spread from the world’s living rooms to the halls of academe, and once the professionals got involved, the puzzle went from insanity-inducing unsolvable to satisfactorily unsolvable. In April 1890 Hermann Schubert, one of the outstanding mathematicians of his day, published in a German newspaper the earliest proof that 13-15-14 was an unsolvable position. Shortly thereafter, the recently founded
American Journal of Mathematics
also published a proof, confirming that half of the total of all starting positions in the Fifteen puzzle will produce a final solution of 13-14-15, and half will end up 13-15-14. The Fifteen puzzle remains the only international craze in which the puzzle does not always have a solution. No wonder it drove people mad.

Like the tangram, the Fifteen puzzle has not totally disappeared. It was the forerunner of the sliding-block puzzles that are still found in toyshops, Christmas crackers and corporate marketing gift packs. In 1974 a Hungariann was devising ways to improve the puzzle when he was struck with the idea of reinventing it in three dimensions. The man, Ernö Rubik, came up with his prototype, the Rubik’s Cube, which went on to become the most successful puzzle in history.

In his 2002 book
The Puzzle Instinct
, the semiotician Marcel Danesi wrote that an intuitive ability to solve puzzles is part of the human condition. When we are presented with a puzzle, he explains, our instincts drive us to find a solution until we are satisfied. From the riddle-asking sphinx of Greek mythology to the detective mystery, puzzles are a common feature across time and cultures. Danesi argues that they are a form of existential therapy, showing us that challenging questions can have precise solutions. Henry Ernest Dudeney, Britain’s greatest puzzle-compiler, described solving puzzles as basic human nature. ‘The fact is that our lives are largely spent in solving puzzles; for what is a puzzle but a perplexing question? And from our childhood upwards we are perpetually asking questions or trying to answer them.’

Puzzles are also a wonderfully concise way of conveying the ‘wow’ factor of maths. Often they require lateral thinking, or rely on counter-intuitive truths. The sense of achievement gained from solving a puzzle is an addictive pleasure; the sense of failure from not solving one almost unbearably frustrating. Publishers realized pretty quickly that fun maths had a market.
Amusing and Entertaining Problems that Can Be Had with Numbers
(
very useful for inquisitive people of all kinds who use arithmetic
) by Claude Gaspard Bachet came out in France in 1612. It included sections on magic squares, card tricks, questions in non-decimal bases, and think-of-a-number problems. Bachet was a serious scholar who translated Diophantus’s
Arithmetica
. But his popular maths book was arguably more influential than his academic work. All subsequent puzzle books are indebted to it, and it has kept its relevance for centuries, republished most recently in 1959. A defining feature of maths, even recreational maths, is that it never goes out of date.