Alex’s Adventures in Numberland (32 page)

Cross-section of Watts’s square drill.

Mathematicians tend to like magic tricks. They can be fun and often conceal interesting theory. Here’s a classic trick that’s also a neat way of appreciating the virtues of algebra. Start by choosing any three-digit number in which the first and last digits differ by at least two – for example, 753. Now, reverse this number to get 357. Subtract the smaller from the larger: 753 – 357 = 396. Finally, add this number to its reverse: 396 + 693. The sum you get is 1089.

Try it again, with a different number, say 421.

The answer is the samIn fact, no matter what three-digit number you start with, you always end up with 1089. As if by magic, 1089 is conjured out of nowhere, a rock in the shifting sands of randomly chosen numbers. Though it is perplexing to think that we get to the same result from any starting point after only a few simple operations, there is an explanation, and we’ll get to it shortly. The mystery of the recurrent 1089 is almost instantly unravelled when the problem is written in symbols rather than in numbers.

While using numbers for the purposes of entertainment has been a consistent theme of mathematical discovery, maths only properly got started as a tool for solving practical problems. The Rhind Papyrus, which dates back to around 1600 bc, is the most comprehensive surviving mathematical document from ancient Egypt. It contains 84 problems covering areas such as surveying, accounting, and how to divide a certain number of loaves among a certain number of men.

The Egyptians stated their problems rhetorically. Problem 30 of the Rhind Papyrus asks, ‘If the scribe says, What is the heap of which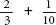
will make ten, let him hear.’ The ‘heap’ is the Egyptian term for the
unknown quantity
, which we now refer to as
x
, the fundamental and essential symbol of modern algebra. Nowadays we would say that Problem 30 is asking: What is the value of
x
such that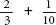
multiplied by
x
is 10. To put it more concisely: What is
x
such that (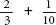
)
x
= 10?

Because the Egyptians didn’t have the symbolic tools that we have now, such as brackets, equal signs, or
x
s, they solved the above question using trial and error. Estimating for the heap, they then worked out the answer. The method is called the ‘rule of false position’ and is rather like playing golf. Once you are on the green, it’s easier to see how to get the ball into the hole. Similarly, once you have an answer, even a wrong answer, you know how to get closer to the right one. By comparison, the modern method of solution is to combine the fractions in the equation with the variable
x
, so that:

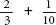x
= 10

Which is the same as:

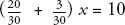
Or:

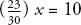
Which further reduces to:

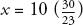
And finally:

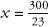
Symbolic notation makes life so much easier.

The Egyptian hieroglyph for addition was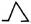
, a pair of legs walking from right to left. Subtraction was
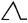, a pair of legs walking from left to right. As number symbols evolved from tally notches to numerals, so the symbols for arithmetical operations also evolved.

Still, the Egyptians had no symbol for the unknown quantity, and neither did Pythagoras or Euclid. For them, maths was geometric, tied to what was constructible. The unknown quantity required a further level of abstraction. The first Greek mathematician to introduce a symbol for the unknown was Diophantus, who used the Greek letter sigma,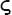
. For the square of the unknown number he used
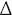^Y
, and for the cube he used K
^Y
. While his notation was a breakthrough in its time, since it meant problems could be expressed more concisely, it was also confusing since, unlike the case with
x
,
x
²
and
x
³
, there was no obvious visual connection between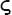
and its powers
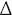^Y
and K
^Y
. Despite his symbols’ shortcomings, however, he is nevertheless remembered as the father of algebra.