Structure and Interpretation of Computer Programs (56 page)

(define (first-agenda-item agenda)
  (if (empty-agenda? agenda)
      (error "Agenda is empty -- FIRST-AGENDA-ITEM")
      (let ((first-seg (first-segment agenda)))
        (set-current-time! agenda (segment-time first-seg))
        (front-queue (segment-queue first-seg)))))

Exercise 3.32.
  The procedures to be run during each time segment of the agenda are
kept in a queue. Thus, the procedures for each segment are called in
the order in which they were added to the agenda (first in, first
out). Explain why this order must be used. In particular, trace the
behavior of an and-gate whose inputs change from 0,1 to 1,0 in the
same segment and say how the behavior would differ if we stored a
segment's procedures in an ordinary list, adding and removing
procedures only at the front (last in, first out).

Computer programs are traditionally organized as
one-directional computations, which perform operations on prespecified
arguments to produce desired outputs. On the other hand, we often
model systems in terms of relations among quantities. For example, a
mathematical model of a mechanical structure might include the
information that the deflection
d
of a metal rod is related to the
force
F
on the rod, the length
L
of the rod, the cross-sectional
area
A
, and the elastic modulus
E
via the equation

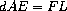
Such an equation is not one-directional. Given any four of the
quantities, we can use it to compute the fifth. Yet translating the
equation into a traditional computer language would force us to choose
one of the quantities to be computed in terms of the other four.
Thus, a procedure for computing the area
A
could not be used to
compute the deflection
d
, even though the computations of
A
and
d
arise from the same equation.
³¹

In this section, we sketch the design of a language that enables us to
work in terms of relations themselves. The primitive elements of the
language are
primitive constraints
, which state that certain
relations hold between quantities. For example,
(adder a b c)
specifies that the quantities
a
,
b
, and
c
must be related by the
equation
a
+
b
=
c
,
(multiplier x y z)
expresses the constraint
x
y
=
z
, and
(constant 3.14 x)
says that the value of
x
must
be 3.14.

Our language provides a means of combining primitive constraints in
order to express more complex relations. We combine constraints by
constructing
constraint networks
, in which constraints are
joined by
connectors
. A connector is an object that “holds” a
value that may participate in one or more constraints. For example,
we know that the relationship between Fahrenheit and Celsius
temperatures is

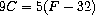
Such a constraint can be thought of as a network consisting of
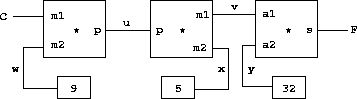
primitive adder, multiplier, and constant constraints
(figure 
3.28
). In the figure, we see on the left a
multiplier box with three terminals, labeled
m
1,
m
2, and
p
.
These connect the multiplier to the rest of the network as follows:
The
m
1 terminal is linked to a connector
C
, which will hold the
Celsius temperature. The
m
2 terminal is linked to a connector
w
, which is also linked to a constant box that holds 9. The
p
terminal, which the multiplier box constrains to be the product of
m
1 and
m
2, is linked to the
p
terminal
of another multiplier box, whose
m
2 is connected to a constant 5 and
whose
m
1 is connected to one of the terms in a sum.

Figure 3.28:
  The relation 9
C
= 5(
F
- 32)
expressed as a constraint network.

Computation by such a network proceeds as follows: When a connector is
given a value (by the user or by a constraint box to which it is
linked), it awakens all of its associated constraints (except for the
constraint that just awakened it) to inform them that it has a value.
Each awakened constraint box then polls its connectors to see if there
is enough information to determine a value for a connector. If so,
the box sets that connector, which then awakens all of its associated
constraints, and so on. For instance, in conversion between
Celsius and Fahrenheit,
w
,
x
, and
y
are immediately set by
the constant boxes to 9, 5, and 32, respectively. The connectors
awaken the multipliers and the adder, which determine that there is
not enough information to proceed. If the user (or some other part of
the network) sets
C
to a value (say 25), the leftmost multiplier
will be awakened, and it will set
u
to 25 · 9 = 225. Then
u
awakens the second multiplier, which sets
v
to 45, and
v
awakens
the adder, which sets
F
to 77.

To use the constraint system to carry out the temperature computation
outlined above, we first create two connectors,
C
and
F
,
by calling the constructor
make-connector
, and link
C
and
F
in an appropriate network:

(define C (make-connector))
(define F (make-connector))
(celsius-fahrenheit-converter C F)
ok

The procedure that creates the network is defined as follows:

(define (celsius-fahrenheit-converter c f)
  (let ((u (make-connector))
        (v (make-connector))
        (w (make-connector))
        (x (make-connector))
        (y (make-connector)))
    (multiplier c w u)
    (multiplier v x u)
    (adder v y f)
    (constant 9 w)
    (constant 5 x)
    (constant 32 y)
    'ok))

This procedure creates the internal connectors
u
,
v
,
w
,
x
, and
y
, and links them as shown in
figure 
3.28
using the primitive constraint
constructors
adder
,
multiplier
, and
constant
. Just
as with the digital-circuit simulator of
section 
3.3.4
, expressing these combinations of
primitive elements in terms of procedures automatically provides our
language with a means of abstraction for compound objects.

To watch the network in action, we can place probes on the connectors
C
and
F
, using a
probe
procedure similar to the one
we used to monitor wires in section 
3.3.4
.
Placing a probe on a connector will cause a message to be printed
whenever the connector is given a value:

(probe "Celsius temp" C)
(probe "Fahrenheit temp" F)

Next we set the value of
C
to 25. (The third argument to
set-value!
tells
C
that this directive comes from the
user
.)

(set-value! C 25 'user)
Probe: Celsius temp = 25
Probe: Fahrenheit temp = 77
done

The probe on
C
awakens and reports the value.
C
also
propagates its value through the network as described above. This
sets
F
to 77, which is reported by the probe on
F
.

Now we can try to set
F
to a new value, say 212:

(set-value! F 212 'user)
Error! Contradiction (77 212)

The connector complains that it has sensed a contradiction: Its value
is 77, and someone is trying to set it to 212. If we really want to
reuse the network with new values, we can tell
C
to forget its
old value:

(forget-value! C 'user)
Probe: Celsius temp = ?
Probe: Fahrenheit temp = ?
done

C
finds that the
user
, who set its value originally, is
now retracting that value, so
C
agrees to lose its value, as
shown by the probe, and informs the rest of the network of this fact.
This information eventually propagates to
F
, which now finds
that it has no reason for continuing to believe that its own value is
77. Thus,
F
also gives up its value, as shown by the probe.

Now that
F
has no value, we are free to set it to 212:

(set-value! F 212 'user)
Probe: Fahrenheit temp = 212
Probe: Celsius temp = 100
done

This new value, when propagated through the network, forces
C
to
have a value of 100, and this is registered by the probe on
C
.
Notice that the very same network is being used to compute
C
given
F
and to compute
F
given 
C
. This
nondirectionality of computation is the distinguishing feature of
constraint-based systems.

The constraint system is implemented via procedural objects with local
state, in a manner very similar to the digital-circuit simulator of
section 
3.3.4
. Although the primitive objects
of the constraint system are somewhat more complex, the overall system
is simpler, since there is no concern about agendas and logic delays.

The basic operations on connectors are the following:

• (has-value? <
  connector
  >)
  tells whether the connector has a value.
  
• (get-value <
  connector
  >)
  returns the connector's current value.
  
• (set-value! <
  connector
  > <
  new-value
  > <
  informant
  >)
  indicates that the informant is requesting the connector to set its
  value to the new value.
  
• (forget-value! <
  connector
  > <
  retractor
  >)
  tells the connector that the retractor is requesting it to forget its value.
  
• (connect <
  connector
  > <
  new-constraint
  >)
  tells the connector to participate in the new constraint.
  

The connectors communicate with the constraints by means of the
procedures
inform-about-value
, which tells the given
constraint that the connector has a value, and
inform-about-no-value
, which tells the constraint that the connector
has lost its value.

Adder
constructs an adder constraint among summand connectors
a1
and
a2
and a
sum
connector. An adder is
implemented as a procedure with local state (the procedure
me
below):