Structure and Interpretation of Computer Programs (58 page)
Read Structure and Interpretation of Computer Programs Online
Authors: Harold Abelson and Gerald Jay Sussman with Julie Sussman

We've seen the power of computational objects with local state as
tools for modeling. Yet, as section
3.1.3
warned, this power extracts a price: the loss of referential
transparency, giving rise to a thicket of questions about sameness and
change, and the need to abandon the substitution model of evaluation in
favor of the more intricate environment model.
The central issue lurking beneath the complexity of state, sameness,
and change is that by introducing assignment we are forced to admit
time
into our computational models. Before we introduced
assignment, all our programs were timeless, in the sense that any
expression that has a value always has the same value. In contrast,
recall the example of modeling withdrawals from a bank account
and returning the resulting balance,
introduced at the beginning of
section
3.1.1
:
(withdraw 25)
75
(withdraw 25)
50
Here successive evaluations of the same expression yield different
values. This behavior arises from the fact that the execution of
assignment statements (in this case, assignments to the variable
balance
) delineates
moments in time
when values change. The
result of evaluating an expression depends not only on the expression
itself, but also on whether the evaluation occurs before or after
these moments. Building models in terms of computational objects with
local state forces us to confront time as an essential concept in
programming.
We can go further in structuring computational models to match our
perception of the physical world. Objects in the world do not change
one at a time in sequence. Rather we perceive them as acting
concurrently
– all at once. So it is often natural to model systems
as collections of computational processes that execute concurrently.
Just as we can make our programs modular by organizing models in
terms of objects with separate local state, it is often appropriate to
divide computational models into parts that evolve separately and
concurrently. Even if the programs are to be executed on a sequential
computer, the practice of writing programs as if they were to be
executed concurrently forces the programmer to avoid inessential
timing constraints and thus makes programs more modular.
In addition to making programs more modular, concurrent computation
can provide a speed advantage over sequential computation. Sequential
computers execute only one operation at a time, so the amount of time
it takes to perform a task is proportional to the total number of
operations performed.
34
However, if it is possible to decompose a problem into pieces that are
relatively independent and need to communicate only rarely, it may be
possible to allocate pieces to separate computing processors,
producing a speed advantage proportional to the number of processors
available.
Unfortunately, the complexities introduced by assignment become even
more problematic in the presence of concurrency. The fact of
concurrent execution, either because the world operates in parallel or
because our computers do, entails additional complexity in our
understanding of time.
On the surface, time seems straightforward. It
is an ordering imposed on events.
35
For any events
A
and
B
, either
A
occurs before
B
,
A
and
B
are simultaneous, or
A
occurs after
B
. For instance,
returning to the bank account example, suppose that Peter withdraws
$10 and Paul withdraws $25 from a
joint account that initially
contains $100, leaving $65 in the account. Depending on the order
of the two withdrawals, the sequence of balances in the account is
either $100 ⟶ $90 ⟶ $65 or
$100 ⟶ $75 ⟶ $65. In a computer implementation
of the banking system, this changing sequence of balances could be
modeled by successive assignments to a variable
balance
.
In complex situations, however, such a view can be problematic.
Suppose that Peter and Paul, and other people besides, are
accessing the same bank account through a network of banking machines
distributed all over the world. The actual sequence of balances in
the account will depend critically on the detailed timing of the
accesses and the details of the communication among the machines.
This indeterminacy in the order of events can pose serious problems in
the design of concurrent systems. For instance, suppose that the
withdrawals made by Peter and Paul are implemented as two separate
processes sharing a common variable
balance
, each process
specified by the procedure given in
section
3.1.1
:
(define (withdraw amount)
(if (>= balance amount)
(begin (set! balance (- balance amount))
balance)
"Insufficient funds"))
If the two processes operate independently, then Peter might test the
balance and attempt to withdraw a legitimate amount. However, Paul
might withdraw some funds in between the time that Peter checks the
balance and the time Peter completes the withdrawal, thus invalidating
Peter's test.
Things can be worse still. Consider the expression
(set! balance (- balance amount))
executed as part of each withdrawal process. This consists of three
steps: (1) accessing the value of the
balance
variable; (2)
computing the new balance; (3) setting
balance
to this new
value. If Peter and Paul's withdrawals execute this statement
concurrently, then the two withdrawals might interleave the order in
which they access
balance
and set it to the new value.
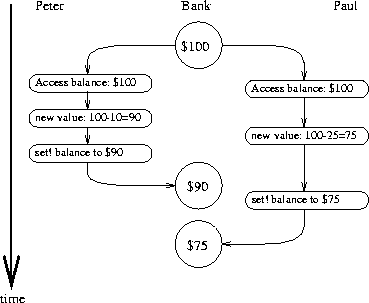
The timing diagram in figure
3.29
depicts an order of
events where
balance
starts at 100, Peter withdraws 10,
Paul withdraws 25, and yet the final value of
balance
is 75. As
shown in the diagram, the reason for this anomaly is that Paul's
assignment of 75 to
balance
is made under the assumption that
the value of
balance
to be decremented is 100. That assumption,
however, became invalid when Peter changed
balance
to 90. This
is a catastrophic failure for the banking system, because the total
amount of money in the system is not conserved. Before the transactions,
the total amount of money was $100. Afterwards, Peter has $10, Paul
has $25, and the bank has $75.
36
The general phenomenon illustrated
here is that several processes may share a
common state variable. What makes this complicated is that more than
one process may be trying to manipulate the shared state at the same
time. For the bank account example, during each transaction, each
customer should be able to act as if the other customers did not
exist. When a customer changes the balance in a way that depends on
the balance, he must be able to assume that, just before the moment of
change, the balance is still what he thought it was.
The above example typifies the subtle bugs that can creep into
concurrent programs. The root of this complexity lies in the
assignments to variables that are shared among the different
processes. We already know that we must be careful in writing
programs that use
set!
, because the results of a computation
depend on the order in which the assignments occur.
37
With concurrent processes we must be especially careful about
assignments, because we may not be able to control the order of the
assignments made by the different processes. If several such changes
might be made concurrently (as with two depositors accessing a joint
account) we need some way to ensure that our system behaves correctly.
For example, in the case of withdrawals from a joint bank account, we
must ensure that money is conserved.
To make concurrent programs behave correctly, we may have to
place some restrictions on concurrent execution.
 |
One possible restriction on concurrency would
stipulate that no two operations that
change any shared state variables can occur at the same time. This is an
extremely stringent requirement. For distributed banking, it would
require the system designer to ensure that only one transaction could
proceed at a time. This would be both inefficient and overly
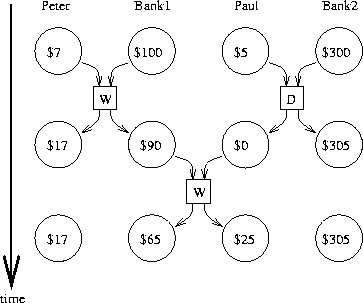
conservative. Figure
3.30
shows Peter and
Paul sharing a bank account, where Paul has a private account as well.
The diagram illustrates two withdrawals from the shared account
(one by Peter and one by Paul) and a deposit to Paul's private account.
38
The two withdrawals from the shared account must not be
concurrent (since both access and update the same account), and Paul's
deposit and withdrawal must not be concurrent (since both access and
update the amount in Paul's wallet).
But there should be no problem
permitting Paul's deposit to his private account to proceed
concurrently with Peter's withdrawal from the shared account.
 |
A less stringent restriction on concurrency would ensure that a
concurrent system produces the same result
as if the processes had run sequentially in some order.
There are two important aspects to this requirement.
First, it does not require the processes to actually run sequentially,
but only to produce results that are the same
as if
they had run
sequentially. For the example in
figure
3.30
, the designer of the bank account
system can safely allow Paul's deposit and Peter's withdrawal to
happen concurrently, because the net result will be the same as if the
two operations had happened sequentially. Second, there may be more
than one possible “correct” result produced by a concurrent program,
because we require only that the result be the same as for
some
sequential order.
For example, suppose that Peter and Paul's joint account starts out
with $100, and Peter deposits $40 while Paul concurrently withdraws
half the money in the account.
Then sequential execution could result in the account balance being
either $70 or $90 (see exercise
3.38
).
39
There are still weaker requirements for correct execution of
concurrent programs. A program for simulating
diffusion (say, the
flow of heat in an object) might consist of a large number of
processes, each one representing a small volume of space, that update
their values concurrently. Each process repeatedly changes its
value to the average of its own value and its neighbors' values.
This algorithm
converges to the right answer independent of the order in which the
operations are done; there is no need for any restrictions on
concurrent use of the shared values.
Exercise 3.38.
Suppose that Peter, Paul, and Mary share a joint bank account that
initially contains $100. Concurrently, Peter deposits $10, Paul
withdraws $20, and Mary withdraws half the money in the account, by
executing the following commands:
| Peter: | (set! balance (+ balance 10)) |
| Paul: | (set! balance (- balance 20)) |
| Mary: | (set! balance (- balance (/ balance 2))) |