Structure and Interpretation of Computer Programs (59 page)
Read Structure and Interpretation of Computer Programs Online
Authors: Harold Abelson and Gerald Jay Sussman with Julie Sussman

a. List all the different possible values for
balance
after these
three transactions have been completed, assuming that the banking
system forces the three processes to run sequentially in some order.
b. What are some other values
that could be produced if the system allows the processes to be interleaved?
Draw timing diagrams like the one in figure
3.29
to
explain how these values can occur.
We've seen that the difficulty in dealing with concurrent processes is
rooted in the need to consider the interleaving of the order of events
in the different processes. For example, suppose we have two
processes, one with three ordered events (
a
,
b
,
c
) and one with three
ordered events (
x
,
y
,
z
). If the two processes run concurrently, with
no constraints on how their execution is interleaved, then there are
20 different possible orderings for the events that are consistent
with the individual orderings for the two processes:
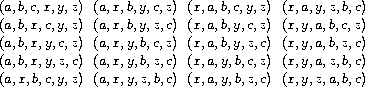
As programmers designing this system, we would have to consider the
effects of each of these 20 orderings and check that each behavior is
acceptable. Such an approach rapidly becomes unwieldy as the numbers
of processes and events increase.
A more practical approach to the design of concurrent systems is to
devise general mechanisms that allow us to constrain the interleaving
of concurrent processes so that we can be sure that the program
behavior is correct. Many mechanisms have been developed for this
purpose. In this section, we describe one of them, the
serializer
.
Serialization implements the following idea: Processes will execute
concurrently, but there will be certain collections of procedures that
cannot be executed concurrently. More precisely, serialization creates
distinguished sets of procedures such that only one execution of a
procedure in each serialized set is permitted to happen at a time.
If some procedure in the set is being executed, then a process that
attempts to execute any procedure in the set will be forced to wait
until the first execution has finished.
We can use serialization to control access to shared variables.
For example, if we want to update a shared variable based on the
previous value of that variable, we put the access to the previous
value of the variable and the assignment of the new value to the
variable in the same procedure. We then ensure that no other
procedure that assigns to the variable can run concurrently with this
procedure by serializing all of these procedures with the same
serializer. This guarantees that the value of the variable cannot be
changed between an access and the corresponding assignment.
To make the above mechanism more concrete, suppose that we have
extended Scheme to include a procedure called
parallel-execute
:
(parallel-execute <
p
1
> <
p
2
>
...
<
p
k
>)
Each <
p
> must be a procedure of no arguments.
Parallel-execute
creates a separate process for each
<
p
>, which applies <
p
> (to no arguments). These processes all
run concurrently.
40
As an example of how this is used, consider
(define x 10)
(parallel-execute (lambda () (set! x (* x x)))
(lambda () (set! x (+ x 1))))
This creates two concurrent processes –
P
1
, which sets
x
to
x
times
x
, and
P
2
, which increments
x
. After
execution is complete,
x
will be left with one of five possible
values, depending on the interleaving of the events of
P
1
and
P
2
:
| 101: | P 1 sets x to 100 and then P 2 increments x to 101. |
| 121: | P 2 increments x to 11 and then P 1 sets x to x times x . |
| 110: | P 2 changes x from 10 to 11 between the two times that P 1 accesses the value of x during the evaluation of (* x x) . |
| 11: | P 2 accesses x , then P 1 sets x to 100, then P 2 sets x . |
| 100: | P 1 accesses x (twice), then P 2 sets x to 11, then P 1 sets x . |
We can constrain the concurrency by using serialized procedures,
which are created by
serializers
. Serializers are constructed by
make-serializer
, whose implementation is given below. A serializer
takes a procedure as argument and returns a serialized procedure that
behaves like the original procedure. All calls to a given serializer
return serialized procedures in the same set.
Thus, in contrast to the example above, executing
(define x 10)
(define s (make-serializer))
(parallel-execute (s (lambda () (set! x (* x x))))
(s (lambda () (set! x (+ x 1)))))
can produce only two possible values for
x
, 101 or 121. The
other possibilities are eliminated, because the execution of
P
1
and
P
2
cannot be interleaved.
Here is a version of the
make-account
procedure from
section
3.1.1
, where the deposits and
withdrawals have been serialized:
(define (make-account balance)
(define (withdraw amount)
(if (>= balance amount)
(begin (set! balance (- balance amount))
balance)
"Insufficient funds"))
(define (deposit amount)
(set! balance (+ balance amount))
balance)
(let ((protected (make-serializer)))
(define (dispatch m)
(cond ((eq? m 'withdraw) (protected withdraw))
((eq? m 'deposit) (protected deposit))
((eq? m 'balance) balance)
(else (error "Unknown request -- MAKE-ACCOUNT"
m))))
dispatch))
With this implementation, two processes cannot be withdrawing from or
depositing into a single account concurrently. This eliminates the source
of the error illustrated in figure
3.29
, where Peter
changes the account balance between the times when Paul accesses the
balance to compute the new value and when Paul actually performs the
assignment. On the other hand, each account has its own serializer,
so that deposits and withdrawals for different accounts can proceed
concurrently.
Exercise 3.39.
Which of the five possibilities in the parallel execution shown above
remain if we instead serialize execution as follows:
(define x 10)
(define s (make-serializer))
(parallel-execute (lambda () (set! x ((s (lambda () (* x x))))))
(s (lambda () (set! x (+ x 1)))))
Exercise 3.40.
Give all possible values of
x
that can result from executing
(define x 10)
(parallel-execute (lambda () (set! x (* x x)))
(lambda () (set! x (* x x x))))
Which of these possibilities remain if we instead use serialized
procedures:
(define x 10)
(define s (make-serializer))
(parallel-execute (s (lambda () (set! x (* x x))))
(s (lambda () (set! x (* x x x)))))
Exercise 3.41.
Ben Bitdiddle worries that it would be better to implement the bank
account as follows (where the commented line has been changed):
(define (make-account balance)
(define (withdraw amount)
(if (>= balance amount)
(begin (set! balance (- balance amount))
balance)
"Insufficient funds"))
(define (deposit amount)
(set! balance (+ balance amount))
balance)
;; continued on next page
(let ((protected (make-serializer)))
(define (dispatch m)
(cond ((eq? m 'withdraw) (protected withdraw))
((eq? m 'deposit) (protected deposit))
((eq? m 'balance)
((protected (lambda () balance))))
; serialized
(else (error "Unknown request -- MAKE-ACCOUNT"
m))))
dispatch))
because allowing unserialized access to the bank balance can result in
anomalous behavior. Do you agree? Is there any scenario that
demonstrates Ben's concern?
Exercise 3.42.
Ben Bitdiddle suggests that it's a waste of time to create a new
serialized procedure in response to every
withdraw
and
deposit
message. He says that
make-account
could be changed so
that the calls to
protected
are done outside the
dispatch
procedure. That is, an account would return the same serialized
procedure (which was created at the same time as the account) each time
it is asked for a withdrawal procedure.
(define (make-account balance)
(define (withdraw amount)
(if (>= balance amount)
(begin (set! balance (- balance amount))
balance)
"Insufficient funds"))
(define (deposit amount)
(set! balance (+ balance amount))
balance)
(let ((protected (make-serializer)))
(let ((protected-withdraw (protected withdraw))
(protected-deposit (protected deposit)))
(define (dispatch m)
(cond ((eq? m 'withdraw) protected-withdraw)
((eq? m 'deposit) protected-deposit)
((eq? m 'balance) balance)
(else (error "Unknown request -- MAKE-ACCOUNT"
m))))
dispatch)))
Is this a safe change to make? In particular, is there any difference in
what concurrency is allowed by these two versions of
make-account
?
Serializers provide a powerful abstraction that helps isolate the
complexities of concurrent programs so that they can be dealt with
carefully and (hopefully) correctly. However, while using serializers
is relatively straightforward when there is only a single shared
resource (such as a single bank account), concurrent programming can
be treacherously difficult when there are multiple shared resources.
To illustrate one of the difficulties that can arise, suppose we wish to swap
the balances in two bank accounts. We access each account to find the
balance, compute the difference between the balances, withdraw this
difference from one account, and deposit it in the other account. We
could implement this as follows:
41
(define (exchange account1 account2)
(let ((difference (- (account1 'balance)
(account2 'balance))))
((account1 'withdraw) difference)
((account2 'deposit) difference)))
This procedure works well when only a single process is trying to do
the exchange. Suppose, however, that Peter and Paul both have access
to accounts
a
1,
a
2, and
a
3, and that
Peter exchanges
a
1 and
a
2 while Paul concurrently exchanges
a
1 and
a
3.
Even with account deposits and withdrawals
serialized for individual accounts (as in the
make-account
procedure shown above in this section),
exchange
can still
produce incorrect results. For example, Peter might compute the
difference in the balances for
a
1 and
a
2, but then Paul
might change the balance in
a
1 before Peter is able to complete
the exchange.
42
For correct behavior, we must arrange for the
exchange
procedure
to lock out any other concurrent accesses to the accounts during the
entire time of the exchange.
One way we can accomplish this is by using both accounts' serializers
to serialize the entire
exchange
procedure.
To do this, we will arrange for access to an account's serializer.
Note that we are deliberately
breaking the modularity of the bank-account object by exposing the
serializer. The following version of
make-account
is identical
to the original version given in
section
3.1.1
, except that a serializer is
provided to protect the balance variable, and the serializer is
exported via message passing: