Structure and Interpretation of Computer Programs (54 page)

Exercise 3.27.
  
Memoization
(also called
tabulation
) is a technique that
enables a procedure to record, in a local table, values that have
previously been computed. This technique can make a vast difference
in the performance of a program. A memoized procedure maintains a
table in which values of previous calls are stored
using as keys the arguments that produced the values. When the
memoized procedure is asked to compute a value, it first checks the
table to see if the value is already there and, if so, just returns
that value. Otherwise, it computes the new value in the ordinary way
and stores this in the table. As an example of memoization, recall
from section 
1.2.2
the exponential process for
computing Fibonacci numbers:

(define (fib n)
  (cond ((= n 0) 0)
        ((= n 1) 1)
        (else (+ (fib (- n 1))
                 (fib (- n 2))))))

The memoized version of the same procedure is

(define memo-fib
  (memoize (lambda (n)
             (cond ((= n 0) 0)
                   ((= n 1) 1)
                   (else (+ (memo-fib (- n 1))
                            (memo-fib (- n 2))))))))

where the memoizer is defined as

(define (memoize f)
  (let ((table (make-table)))
    (lambda (x)
      (let ((previously-computed-result (lookup x table)))
        (or previously-computed-result
            (let ((result (f x)))
              (insert! x result table)
              result))))))

Draw an environment diagram to analyze the computation of
(memo-fib 3)
. Explain why
memo-fib
computes the
n
th
Fibonacci number in a number of steps proportional to
n
.
Would the scheme still
work if we had simply defined
memo-fib
to be
(memoize
fib)
?

Designing complex digital systems, such as computers, is an important
engineering activity. Digital systems are constructed by
interconnecting simple elements. Although the behavior of these
individual elements is simple, networks of them can have very complex
behavior. Computer simulation of proposed circuit designs is an
important tool used by digital systems engineers. In this section we
design a system for performing digital logic simulations. This system
typifies a kind of program called an
event-driven simulation
, in
which actions (“events”) trigger further events that happen at a
later time, which in turn trigger more events, and so so.

Our computational model of a circuit will be composed of objects that
correspond to the elementary components from which the circuit is
constructed. There are
wires
, which carry
digital signals
. A
digital signal may at any moment have only one of two possible values,
0 and 1. There are also various types of digital
function
boxes
, which connect wires carrying input signals to other output
wires. Such boxes produce output signals computed from their input
signals. The output signal is
delayed by a time that depends on the
type of the function box. For example, an
inverter
is a
primitive function box that inverts its input. If the
input signal to an inverter changes to 0, then one inverter-delay
later the inverter will change its output signal to 1. If the input
signal to an inverter changes to 1, then one inverter-delay later the
inverter will change its output signal to 0. We draw an inverter
symbolically as in figure 
3.24
. An
and-gate
,
also shown in figure 
3.24
, is a primitive function
box with two inputs and one output. It drives its output signal to a
value that is the
logical and
of the inputs. That is, if both
of its input signals become 1, then one and-gate-delay time later the
and-gate will force its output signal to be 1; otherwise the output
will be 0. An
or-gate
is a similar two-input primitive function
box that drives its output signal to a value that is the
logical
or
of the inputs. That is, the output will become 1 if at least one
of the input signals is 1; otherwise the output will become 0.

Figure 3.24:
  Primitive functions in the digital logic simulator.

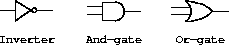We can connect primitive functions together to construct more complex
functions. To accomplish this we wire the outputs of some
function boxes to the inputs of other function boxes. For example,
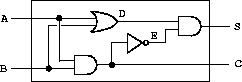
the
half-adder
circuit shown in figure 
3.25
consists of an
or-gate, two and-gates, and an inverter. It takes two input signals,
A and B, and has two output signals, S and C. S will become 1
whenever precisely one of A and B is 1, and C will become 1 whenever A
and B are both 1. We can see from the figure that, because of the
delays involved, the outputs may be generated at different times.
Many of the difficulties in the design of digital circuits arise from
this fact.

Figure 3.25:
  A half-adder circuit.

We will now build a program for modeling the digital logic circuits we
wish to study. The program will construct computational objects
modeling the wires, which will “hold” the signals. Function boxes
will be modeled by procedures that enforce the correct relationships
among the signals.

One basic element of our simulation will be a procedure
make-wire
, which constructs wires. For example, we can construct six
wires as follows:

(define a (make-wire))
(define b (make-wire))
(define c (make-wire))
(define d (make-wire))
(define e (make-wire))
(define s (make-wire))

We attach a function box to a set of wires by calling a procedure that
constructs that kind of box. The arguments to the constructor
procedure are the wires to be attached to the box. For example, given
that we can construct and-gates, or-gates, and inverters, we can wire
together the half-adder shown in figure 
3.25
:

(or-gate a b d)
ok
(and-gate a b c)
ok
(inverter c e)
ok
(and-gate d e s)
ok

Better yet, we can explicitly name this operation by defining a procedure
half-adder
that constructs this circuit, given the four
external wires to be attached to the half-adder:

(define (half-adder a b s c)
  (let ((d (make-wire)) (e (make-wire)))
    (or-gate a b d)
    (and-gate a b c)
    (inverter c e)
    (and-gate d e s)
    'ok))

The advantage of making this definition is that we can use
half-adder
itself as a building block in creating more complex
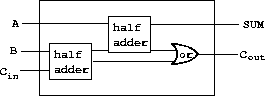
circuits. Figure 
3.26
, for example, shows a
full-adder
composed of two half-adders and an or-gate.
²⁶
We can construct a full-adder
as follows:

(define (full-adder a b c-in sum c-out)
  (let ((s (make-wire))
        (c1 (make-wire))
        (c2 (make-wire)))
    (half-adder b c-in s c1)
    (half-adder a s sum c2)
    (or-gate c1 c2 c-out)
    'ok))

Having defined
full-adder
as a procedure, we can now use it as a
building block for creating still more complex circuits. (For
example, see exercise 
3.30
.)

Figure 3.26:
  A full-adder circuit.

In essence, our simulator provides us with the tools to construct a
language of circuits. If we adopt the general perspective on
languages with which we approached the study of Lisp in
section 
1.1
,
we can say that the primitive function boxes form the primitive
elements of the language, that wiring boxes together provides a means
of combination, and that specifying wiring patterns as procedures
serves as a means of abstraction.

The primitive function boxes implement the “forces” by which a
change in the signal on one wire influences the signals on other
wires. To build function boxes, we use the following operations on
wires:

• (get-signal <
  wire
  >)
  returns the current value of the signal on the wire.
  
• (set-signal! <
  wire
  > <
  new value
  >)
  changes the value of the signal on the wire to the new value.
  
• (add-action! <
  wire
  > <
  procedure of no arguments
  >)
  asserts that the designated procedure should be run whenever the
  signal on the wire changes value. Such procedures are the vehicles by
  which changes in the signal value on the wire are communicated to
  other wires.
  

In addition, we will make use of a procedure
after-delay
that
takes a time delay and a procedure to be run and executes the
given procedure after the given delay.

Using these procedures, we can define the primitive digital logic
functions. To connect an input to an output through an inverter, we
use
add-action!
to associate with the input wire a procedure
that will be run whenever the signal on the input wire changes value.
The procedure computes the
logical-not
of the input signal, and
then, after one
inverter-delay
, sets the output signal to be
this new value:

(define (inverter input output)
  (define (invert-input)
    (let ((new-value (logical-not (get-signal input))))
      (after-delay inverter-delay
                   (lambda ()
                     (set-signal! output new-value)))))
  (add-action! input invert-input)
  'ok)
(define (logical-not s)
  (cond ((= s 0) 1)
        ((= s 1) 0)
        (else (error "Invalid signal" s))))

An and-gate is a little more complex. The action procedure must be run if
either of the inputs to the gate changes. It computes the
logical-and
(using a procedure analogous to
logical-not
) of the
values of the signals on the input wires and sets up a change to the
new value to occur on the output wire after one
and-gate-delay
.

(define (and-gate a1 a2 output)
  (define (and-action-procedure)
    (let ((new-value
           (logical-and (get-signal a1) (get-signal a2))))
      (after-delay and-gate-delay
                   (lambda ()
                     (set-signal! output new-value)))))
  (add-action! a1 and-action-procedure)
  (add-action! a2 and-action-procedure)
  'ok)

Exercise 3.28.
  
Define an or-gate as a primitive function box. Your
or-gate
constructor should be similar to
and-gate
.

Exercise 3.29.
  
Another way to construct an or-gate is as a compound digital logic
device, built from and-gates and inverters. Define a procedure
or-gate
that accomplishes this. What is the delay time of the
or-gate in terms of
and-gate-delay
and
inverter-delay
?