Structure and Interpretation of Computer Programs (52 page)

One way to detect sharing in list structures is to use the predicate
eq?
, which we introduced in section 
2.3.1
as a
way to test whether two symbols are equal. More generally,
(eq?
x y)
tests whether
x
and
y
are the same object (that is,
whether
x
and
y
are equal as pointers). Thus, with
z1
and
z2
as defined in figures 
3.16
and 
3.17
,
(eq? (car z1) (cdr z1))
is true and
(eq? (car z2) (cdr z2))
is false.

As will be seen in the following sections, we can exploit sharing to
greatly extend the repertoire of data structures that can be
represented by pairs. On the other hand, sharing can also be
dangerous, since modifications made to structures will also affect
other structures that happen to share the modified parts. The
mutation operations
set-car!
and
set-cdr!
should be used
with care; unless we have a good understanding of how our data objects
are shared, mutation can have unanticipated results.
²⁰

Exercise 3.15.
  Draw box-and-pointer diagrams to explain the effect of
set-to-wow!
on the structures
z1
and
z2
above.

Exercise 3.16.
  Ben Bitdiddle decides to write a procedure to count the number of
pairs in any list structure. “It's easy,” he reasons. “The number
of pairs in any structure is the number in the
car
plus the
number in the
cdr
plus one more to count the current pair.”
So Ben writes the following procedure:

(define (count-pairs x)
  (if (not (pair? x))
      0
      (+ (count-pairs (car x))
         (count-pairs (cdr x))
         1)))

Show that this procedure is not correct. In particular, draw
box-and-pointer diagrams representing list structures made up of
exactly three pairs for which Ben's procedure would return 3; return
4; return 7; never return at all.

Exercise 3.17.
  Devise a correct version of the
count-pairs
procedure of
exercise 
3.16
that returns the number of distinct
pairs in any structure. (Hint: Traverse the structure, maintaining an
auxiliary data structure that is used to keep track of which pairs
have already been counted.)

Exercise 3.18.
  
Write a procedure that examines a list and determines whether it
contains a cycle, that is, whether a program that tried to find the
end of the list by taking successive
cdr
s would go into an
infinite loop. Exercise 
3.13
constructed such lists.

Exercise 3.19.
  Redo exercise 
3.18
using an algorithm that takes only a
constant amount of space. (This requires a very clever idea.)

When we introduced compound data, we observed in
section 
2.1.3
that pairs can be represented purely in terms
of procedures:

(define (cons x y)
  (define (dispatch m)
    (cond ((eq? m 'car) x)
          ((eq? m 'cdr) y)
          (else (error "Undefined operation -- CONS" m))))
  dispatch)
(define (car z) (z 'car))
(define (cdr z) (z 'cdr))

The same observation is true for mutable data. We can implement
mutable data objects as procedures using assignment and local state.
For instance, we can extend the above pair implementation to handle
set-car!
and
set-cdr!
in a manner analogous to the way
we implemented bank accounts using
make-account
in
section 
3.1.1
:

(define (cons x y)
  (define (set-x! v) (set! x v))
  (define (set-y! v) (set! y v))
  (define (dispatch m)
    (cond ((eq? m 'car) x)
          ((eq? m 'cdr) y)
          ((eq? m 'set-car!) set-x!)
          ((eq? m 'set-cdr!) set-y!)
          (else (error "Undefined operation -- CONS" m))))
  dispatch)
(define (car z) (z 'car))
(define (cdr z) (z 'cdr))
(define (set-car! z new-value)
  ((z 'set-car!) new-value)
  z)
(define (set-cdr! z new-value)
  ((z 'set-cdr!) new-value)
  z)

Assignment is all that is needed, theoretically, to account for the
behavior of mutable data. As soon as we admit
set!
to our
language, we raise all the issues, not only of assignment, but of
mutable data in general.
²¹

Exercise 3.20.
  Draw environment diagrams to illustrate the evaluation of the sequence
of expressions

(define x (cons 1 2))
(define z (cons x x))
(set-car! (cdr z) 17)
(car x)
17

using the procedural implementation of pairs given above. (Compare
exercise 
3.11
.)

The mutators
set-car!
and
set-cdr!
enable us to use
pairs to construct data structures that cannot be built with
cons
,
car
, and
cdr
alone. This section shows how to use
pairs to represent a data structure called a queue. Section 
3.3.3
will show how to represent data structures called tables.

A
queue
is a sequence in which items are inserted at one end
(called the
rear
of the queue) and deleted from the other end
(the
front
). Figure 
3.18
shows an initially empty
queue in which the items
a
and
b
are inserted. Then
a
is removed,
c
and
d
are inserted, and
b
is
removed. Because items are always removed in the order in which they
are inserted, a queue is sometimes called a
FIFO
(first in,
first out) buffer.

In terms of data abstraction, we can regard a queue as defined by the
following set of operations:

• a constructor:
  (make-queue)
  returns an empty queue (a queue containing no items).
  
• two selectors:
  (empty-queue? <
  queue
  >)
  tests if the queue is empty.
  (front-queue <
  queue
  >)
  returns the object at the front of
  the queue, signaling an error if the queue is empty; it does not
  modify the queue.
  
• two mutators:
  (insert-queue! <
  queue
  > <
  item
  >)
  inserts the item at the rear of the queue and returns the modified
  queue as its value.
  (delete-queue! <
  queue
  >)
  removes the item at the
  front of the queue and returns the modified queue as its value,
  signaling an error if the queue is empty before the deletion.
  

Because a queue is a sequence of items, we could certainly represent
it as an ordinary list; the front of the queue would be the
car
of the list, inserting an item in the queue would amount to appending
a new element at the end of the list, and deleting an item from the
queue would just be taking the
cdr
of the list. However, this
representation is inefficient, because in order to insert an item we
must scan the list until we reach the end. Since the only method we
have for scanning a list is by successive
cdr
operations, this
scanning requires θ(
n
) steps for a list of
n
items. A simple
modification to the list representation overcomes this disadvantage by
allowing the queue operations to be implemented so that they require
θ(1) steps; that is, so that the number of steps
needed is independent of the length of the queue.

The difficulty with the list representation arises from the need to
scan to find the end of the list. The reason we need to scan is that,
although the standard way of representing a list as a chain of pairs
readily provides us with a pointer to the beginning of the list, it
gives us no easily accessible pointer to the end. The modification
that avoids the drawback is to represent the queue as a list, together
with an additional pointer that indicates the final pair in the list.
That way, when we go to insert an item, we can consult the rear
pointer and so avoid scanning the list.

A queue is represented, then, as a pair of pointers,
front-ptr
and
rear-ptr
, which indicate, respectively, the first and last
pairs in an ordinary list. Since we would like the queue to be an
identifiable object, we can use
cons
to combine the two
pointers. Thus, the queue itself will be the
cons
of the two
pointers. Figure 
3.19
illustrates this
representation.

Figure 3.19:
  Implementation of a queue as a list with front and rear
pointers.

To define the queue operations we use the following procedures, which
enable us to select and to modify the front and rear pointers of a
queue:

(define (front-ptr queue) (car queue))
(define (rear-ptr queue) (cdr queue))
(define (set-front-ptr! queue item) (set-car! queue item))
(define (set-rear-ptr! queue item) (set-cdr! queue item))

Now we can implement the actual queue operations. We will consider a
queue to be empty if its front pointer is the empty list:

(define (empty-queue? queue) (null? (front-ptr queue)))

The
make-queue
constructor returns, as an initially empty queue,
a pair whose
car
and
cdr
are both the empty list:

(define (make-queue) (cons '() '()))

To select the item at the front of the queue, we return the
car
of the pair indicated by the front pointer:

(define (front-queue queue)
  (if (empty-queue? queue)
      (error "FRONT called with an empty queue" queue)
      (car (front-ptr queue))))

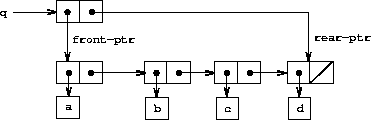
To insert an item in a queue, we follow the method whose result is
indicated in figure 
3.20
. We first create a new
pair whose
car
is the item to be inserted and whose
cdr
is
the empty list. If the queue was initially empty, we set the front and
rear pointers of the queue to this new pair. Otherwise, we modify the
final pair in the queue to point to the new pair, and also set the
rear pointer to the new pair.

Figure 3.20:
  Result of using
(insert-queue! q 'd)
on the queue of figure 
3.19
.

(define (insert-queue! queue item)
  (let ((new-pair (cons item '())))
    (cond ((empty-queue? queue)
           (set-front-ptr! queue new-pair)
           (set-rear-ptr! queue new-pair)
           queue)
          (else
           (set-cdr! (rear-ptr queue) new-pair)
           (set-rear-ptr! queue new-pair)
           queue)))) 

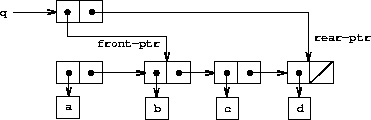
To delete the item at the front of the queue, we merely modify the
front pointer so that it now points at the second item in the queue,
which can be found by following the
cdr
pointer of the first
item (see figure 
3.21
):
²²

Figure 3.21:
  Result of using
(delete-queue! q)
on
the queue of figure 
3.20
.