Structure and Interpretation of Computer Programs (51 page)

Figure 3.13:
  Effect of
(set-car! x y)
on the lists in
figure 
3.12
.

Figure 3.14:
  Effect of
(define z (cons y (cdr x)))
on
the lists in figure 
3.12
.

Figure 3.15:
  Effect of
(set-cdr! x y)
on the lists in
figure 
3.12
.

The primitive mutators for pairs are
set-car!
and
set-cdr!
.
Set-car!
takes two arguments, the first of which
must be a pair. It modifies this pair, replacing the
car
pointer by a pointer to the second argument of
set-car!
.
¹⁶

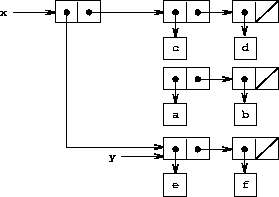
As an example, suppose that
x
is bound to the list
((a b) c
d)
and
y
to the list
(e f)
as illustrated in
figure 
3.12
. Evaluating the expression
(set-car!
x y)
modifies the pair to which
x
is bound, replacing its
car
by the value of
y
. The result of the operation is shown in
figure 
3.13
. The structure
x
has been modified and
would now be printed
as
((e f) c d)
. The
pairs representing the list
(a b)
, identified by the pointer
that was replaced, are now detached from the original
structure.
¹⁷

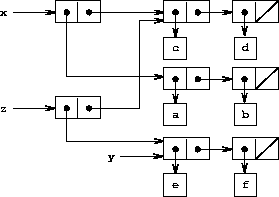
Compare figure 
3.13
with figure 
3.14
,
which illustrates the result of executing
(define z (cons y (cdr
x)))
with
x
and
y
bound to the original lists of
figure 
3.12
. The variable
z
is now bound to a
new pair created by the
cons
operation; the list to which
x
is bound is unchanged.

The
set-cdr!
operation is similar to
set-car!
. The
only difference is that the
cdr
pointer of the pair, rather than
the
car
pointer, is replaced. The effect of executing
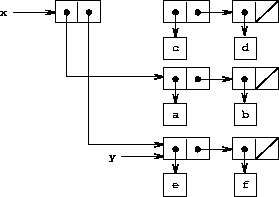
(set-cdr! x y)
on the lists of figure 
3.12
is shown
in figure 
3.15
.
Here the
cdr
pointer of
x
has been replaced by the pointer
to
(e f)
. Also, the list
(c d)
, which used to be the
cdr
of
x
, is now detached from the structure.

Cons
builds new list structure by creating new pairs, while
set-car!
and
set-cdr!
modify existing pairs. Indeed, we
could implement
cons
in terms of the two mutators, together with
a procedure
get-new-pair
, which returns a new pair that is not
part of any existing list structure. We obtain the new pair, set its
car
and
cdr
pointers to the designated objects, and return
the new pair as the result of the
cons
.
¹⁸

(define (cons x y)
  (let ((new (get-new-pair)))
    (set-car! new x)
    (set-cdr! new y)
    new))

Exercise 3.12.
  
The following procedure for appending lists was introduced in
section 
2.2.1
:

(define (append x y)
  (if (null? x)
      y
      (cons (car x) (append (cdr x) y))))

Append
forms a new list by successively
cons
ing the
elements of
x
onto
y
. The procedure
append!
is
similar to
append
, but it is a mutator rather than a constructor.
It appends the lists by splicing them together, modifying the final
pair of
x
so that its
cdr
is now
y
.
(It is an error to call
append!
with an empty 
x
.)

(define (append! x y)
  (set-cdr! (last-pair x) y)
  x)

Here
last-pair
is a procedure that returns the last pair in its
argument:

(define (last-pair x)
  (if (null? (cdr x))
      x
      (last-pair (cdr x))))

Consider the interaction

(define x (list 'a 'b))
(define y (list 'c 'd))
(define z (append x y))
z
(a b c d)
(cdr x)
<
response
>
(define w (append! x y))
w
(a b c d)
(cdr x)
<
response
>

What are the missing <
response
>s?
Draw box-and-pointer diagrams to explain your answer.

Exercise 3.13.
  
Consider the following
make-cycle
procedure, which uses the
last-pair
procedure defined in exercise 
3.12
:

(define (make-cycle x)
  (set-cdr! (last-pair x) x)
  x)

Draw a box-and-pointer diagram that shows the structure
z
created by

(define z (make-cycle (list 'a 'b 'c)))

What happens if we try to compute
(last-pair z)
?

Exercise 3.14.
  The following procedure is quite useful, although obscure:

(define (mystery x)
  (define (loop x y)
    (if (null? x)
        y
        (let ((temp (cdr x)))
          (set-cdr! x y)
          (loop temp x))))
  (loop x '()))

Loop
uses the “temporary” variable
temp
to hold
the old value of the
cdr
of
x
, since the
set-cdr!
on the next line destroys the
cdr
. Explain what
mystery
does in general. Suppose
v
is defined by
(define v (list 'a
'b 'c 'd))
. Draw the box-and-pointer diagram that represents the list
to which
v
is bound. Suppose that we now evaluate
(define
w (mystery v))
. Draw box-and-pointer diagrams that show the
structures
v
and
w
after evaluating this expression. What
would be printed as the values of
v
and
w
?

We mentioned in section 
3.1.3
the theoretical
issues of “sameness” and “change” raised by the introduction of
assignment. These issues arise in practice when individual pairs are
shared
among different data objects. For example, consider the
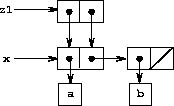
structure formed by

(define x (list 'a 'b))
(define z1 (cons x x))

As shown in figure 
3.16
,
z1
is a pair whose
car
and
cdr
both point to the same pair
x
. This sharing
of
x
by the
car
and
cdr
of
z1
is a consequence
of the straightforward way in which
cons
is implemented. In
general, using
cons
to construct lists will result in an
interlinked structure of pairs in which many individual pairs are
shared by many different structures.

Figure 3.16:
  The list
z1
formed by
(cons x x)
.

Figure 3.17:
  The list
z2
formed by
(cons (list 'a 'b) (list 'a 'b))
.

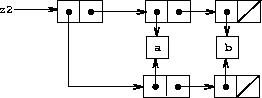In contrast to figure 
3.16
, figure 
3.17
shows
the structure created by

(define z2 (cons (list 'a 'b) (list 'a 'b)))

In this structure, the pairs in the two
(a b)
lists are
distinct, although the actual symbols are shared.
¹⁹

When thought of as a list,
z1
and
z2
both represent “the
same” list,
((a b) a b)
. In general, sharing is completely
undetectable if we operate on lists using only
cons
,
car
,
and
cdr
. However, if we allow mutators on list structure,
sharing becomes significant. As an example of the difference that
sharing can make, consider the following procedure, which modifies the
car
of the structure to which it is applied:

(define (set-to-wow! x)
  (set-car! (car x) 'wow)
  x)

Even though
z1
and
z2
are “the same” structure,
applying
set-to-wow!
to them yields different results. With
z1
, altering the
car
also changes the
cdr
, because
in
z1
the
car
and the
cdr
are the same pair. With
z2
, the
car
and
cdr
are distinct, so
set-to-wow!
modifies only the
car
:

z1
((a b) a b)
(set-to-wow! z1)
((wow b) wow b)
z2
((a b) a b)
(set-to-wow! z2)
((wow b) a b)